题目内容
4.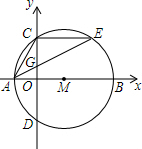 如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C,
如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C,D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8.
(1)求点C的坐标;
(2)连接MG,BC,求证:MG∥BC.
分析 (1)连结MC交AE于H,如图,由于C为弧AE的中点,根据垂径定理得到MC⊥AE,AH=EH=$\frac{1}{2}$AE=4,再证明△AMH≌△CMO得到AH=OC=4,于是可得到C点坐标;
(2)延长MG交AC于N,如图,由于AB⊥CD,根据垂径定理得到弧AC=弧AD,加上C为弧AE的中点,则弧AD=弧CE,根据圆周角定理得∠CAE=∠ACD,则GA=GC,根据垂直平分线定理的逆定理可判断MN垂直平分AC,
接着根据圆周角定理由AB为直径得到∠ACB=90°,然后根据平行线的判定方法即可得到MG∥BC.
解答 (1)证明:连结MC交AE于H,如图,
∵C为弧AE的中点,
∴MC⊥AE,AH=EH=$\frac{1}{2}$AE=4,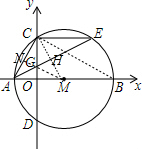
在△AMH和△CMO中
$\left\{\begin{array}{l}{∠AHM=∠COM}\\{∠AMH=∠CMO}\\{MA=MC}\end{array}\right.$,
∴△AMH≌△CMO,
∴AH=OC=4,
∴C点坐标为(0,4);
(2)证明:延长MG交AC于N,如图,
∵AB⊥CD,
∴弧AC=弧AD,
而C为弧AE的中点,
∴弧AD=弧CE,
∴∠CAE=∠ACD,
∴GA=GC,
而MC=MA,
∴MN垂直平分AC,
∵AB为直径,
∴∠ACB=90°,
∴BC⊥AC,
∴MG∥BC.
点评 本题考查了圆的综合题:熟练掌握垂径定理和圆周角定理;会运用全等三角形的判定与性质证明线段相等;理解坐标与图形性质.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
1.与-3的积为1的数是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
6. 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )| A. | 0<x<1 | B. | -1<x<0 | C. | x<0或x>1 | D. | x<-1或x>0 |
 周老师和夏老师两人从A地出发,骑自行车沿同一条路行驶到B地.夏老师因为有事,在A地停留0.5小时后出发,1小时后他们相遇,两人约定,谁先到B地就在原地等待.他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示.
周老师和夏老师两人从A地出发,骑自行车沿同一条路行驶到B地.夏老师因为有事,在A地停留0.5小时后出发,1小时后他们相遇,两人约定,谁先到B地就在原地等待.他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示. 将一张长方形纸片折叠后如图,若∠2=45°,则∠1,∠3,∠4的度数是多少?
将一张长方形纸片折叠后如图,若∠2=45°,则∠1,∠3,∠4的度数是多少?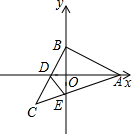 如图,在直角坐标系中,点A(8,0),点B(0,4),点C(-4,-4),连接BC与x轴相交于点D,连接AC与y轴相交于点E,连接DE.
如图,在直角坐标系中,点A(8,0),点B(0,4),点C(-4,-4),连接BC与x轴相交于点D,连接AC与y轴相交于点E,连接DE.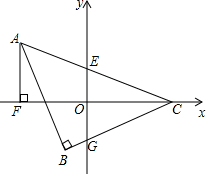 如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.
如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.