题目内容
13.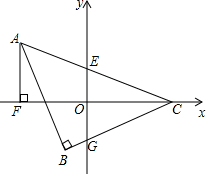 如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.
如图,将△ABC放置在平面直角坐标系中,点C在x轴上,∠ABC=90°,∠ACB=45°,AB=BC,x轴平分∠ACB,AC交y轴于点E,BC交y轴于点G,AB交x轴于点H.(1)求证:∠FAH=∠HCB;
(2)求证:AF=$\frac{1}{2}$CH.
分析 (1)先判断△ABC为等腰直角三角形得到∠ABC=90°,根据根据对顶角相等和三角形内角和定理可证明∠FAH=∠HCB;
(2)延长AF与CB,它们相交于点M,如图,利用“ASA”可证明△ABM≌△CBH,则AM=CH,再利用等腰三角形的判定与性质得到AF=$\frac{1}{2}$AM,于是有AF=$\frac{1}{2}$CH.
解答 证明:(1)∵ACB=45°,AB=BC,
∴△ABC为等腰直角三角形,
∴∠ABC=90°,
∵∠AFC=∠ABC=90°,∠1=∠2,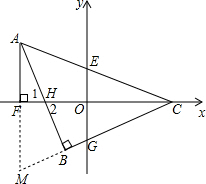
∴∠FAH=∠HCB;
(2)延长AF与CB,它们相交于点M,如图,
在△ABM和△CBH中,
$\left\{\begin{array}{l}{∠MAB=∠HCB}\\{AB=CB}\\{∠ABM=∠CBH}\end{array}\right.$,
∴△ABM≌△CBH,
∴AM=CH,
∵x轴平分∠ACB,即CF平分∠ACM,
∵CF⊥AM,
∴AF=FM,即AF=$\frac{1}{2}$AM,
∴AF=$\frac{1}{2}$CH.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.解决本题的关键是构建△ABM与△CBH全等.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
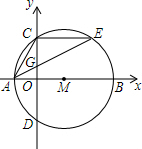 如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C,
如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C, 如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,延长BA、CE相交于点F.求证:BD=2CE.
如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,延长BA、CE相交于点F.求证:BD=2CE.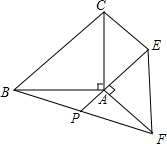 如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.
如图,等腰直角△ABC和等腰直角△AEF,∠BAC=∠EAF=90°,连结CE、BF,延长EA交BF于P,当点P为BF的中点时,求$\frac{CE}{AP}$的值.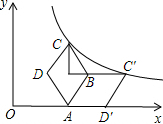 如图,菱形ABCD的顶点A在x轴的正半轴上,∠DAB=60°,若将菱形ABCD沿AB翻折得到菱形ABC′D′,D′点恰好落在x轴上,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C和C′,过C作CE垂直C′B的延长线于E,连接CC′,已知S△CEC′=$\frac{3\sqrt{3}}{2}$,则k的值是( )
如图,菱形ABCD的顶点A在x轴的正半轴上,∠DAB=60°,若将菱形ABCD沿AB翻折得到菱形ABC′D′,D′点恰好落在x轴上,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C和C′,过C作CE垂直C′B的延长线于E,连接CC′,已知S△CEC′=$\frac{3\sqrt{3}}{2}$,则k的值是( )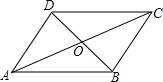 已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.