题目内容
14.观察下列关于自然数的等式:2×4-12+1=8
3×5-22+1=12
4×6-32+1=16
5×7-42+1=20
…
利用等式的规律,解答下列问题:
(1)若等式8×10-a2+1=b(a,b都为自然数)具有以上规律,则a=7,a+b=39.
(2)写出第n个等式(用含n的代数式表示),并验证它的正确性.
分析 (1)等式左边第一个因数比幂底数大1、第二个因数比幂的底数大3,而等式右边是第一个因数的4倍.
(2)用n表示幂的底数,第一、二两因数为(n+1)、(n+3),而等式右边则为4(n+1),可得等式.
解答 解:(1)以上等式的规律是:
等式左边第一个因数比幂底数大1、第二个因数比幂的底数大3,而等式右边是第一个因数的4倍;
∵8×10-a2+1=b,
∴a=8-1=7,b=4×8=32;
则a+b=39,
所以答案为:7,39.
(2)第n个等式为:(n+1)(n+3)-n2+1=4(n+1);
∵左边=n2+3n+n+3-n2+1
=4n+4
=4(n+1)=右边
∴等式成立.
点评 本题主要考查数字变化规律及数字间的联系,并涉及整式的化简运算能力.

练习册系列答案
相关题目
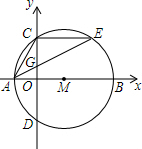 如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C,
如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C,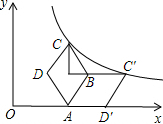 如图,菱形ABCD的顶点A在x轴的正半轴上,∠DAB=60°,若将菱形ABCD沿AB翻折得到菱形ABC′D′,D′点恰好落在x轴上,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C和C′,过C作CE垂直C′B的延长线于E,连接CC′,已知S△CEC′=$\frac{3\sqrt{3}}{2}$,则k的值是( )
如图,菱形ABCD的顶点A在x轴的正半轴上,∠DAB=60°,若将菱形ABCD沿AB翻折得到菱形ABC′D′,D′点恰好落在x轴上,双曲线y=$\frac{k}{x}$(x>0)恰好经过点C和C′,过C作CE垂直C′B的延长线于E,连接CC′,已知S△CEC′=$\frac{3\sqrt{3}}{2}$,则k的值是( )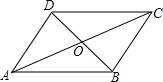 已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.