题目内容
19.已知:抛物线y=x2+(2m-1)x+m2-1经过坐标原点,且当x<0时,y随x的增大而减小.(1)求抛物线的解析式;
(2)结合图象写出y<0时,对应的x的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,直接写出矩形ABCD的周长.
分析 (1)根据图象过原点,可得关于m的方程,根据解方程,可得答案;
(2)根据函数与不等式的关系:图象位于x轴下方部分是不等式的解集,可得答案;
(3)根据平行于x轴的直线与抛物线的交点关于对称轴对称,可得A、D点关于对称轴对称,根据AB⊥x轴于点B,DC⊥x轴于点C,可得B点坐标,根据自变量与函数值的对应关系,可得A点坐标,根据矩形的周长公式,可得答案.
解答 解:(1)由y=x2+(2m-1)x+m2-1经过坐标原点,得
m2-1=0,解得m=1或m=-1.
当x<0时,y随x的增大而减小,
得m=-1.
抛物线的解析式y=x2-3x;
(2)由图象1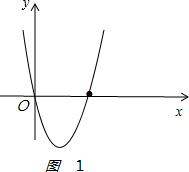 ,得
,得
位于x轴下方的部分,
y<0时,对应的x的取值范围0<x<3;
(3)如图2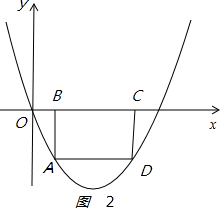 ,
,
由AD∥x轴,得
A、D关于对称轴x=1.5对称,
B、C关于对称轴x=1.5对称,且BC=1,得
1.5-0.5=1,即B(1,0).
当x=1时,y=1-3=-2,
即A(1,-2).
矩形ABCD的周长为2(AB+BC)=2×(2+1)=6.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,利用函数与不等式的关系:图象位于x轴下方部分是不等式的解集;利用平行于x轴的直线与抛物线的交点关于对称轴对称得出A、D关于对称轴对称是解题关键.

练习册系列答案
相关题目
7.下列几何体中,截面图不可能是三角形的有( )
①圆锥;②圆柱;③长方体;④球.
①圆锥;②圆柱;③长方体;④球.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C,
如图,在平面直角坐标系xOy中,点M在x轴上,⊙M交x轴于A,B两点,交y轴于C, 如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,延长BA、CE相交于点F.求证:BD=2CE.
如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,延长BA、CE相交于点F.求证:BD=2CE. 已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.
已知:如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长长8cm,求AB和BC的长.