题目内容
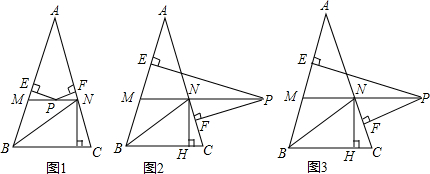
 △ABC内接于⊙O且AB>AC,直径PD⊥BC,过P作PE⊥AB于E,PF⊥CA的延长线于F,求证:AE=
△ABC内接于⊙O且AB>AC,直径PD⊥BC,过P作PE⊥AB于E,PF⊥CA的延长线于F,求证:AE=| 1 |
| 2 |
考点:全等三角形的判定与性质,圆周角定理
专题:计算题
分析:连接PA,PB,PC,由直径PD垂直于BC,利用垂径定理得到PD平分BC,即PD垂直平分BC,得到PB=PC,利用等边对等角得到一对角相等,由圆内接四边形外角等于它的内对角得到一对角相等,再利用同弧所对的圆周角相等得到一对角相等,等量代换得到∠PAF=∠PAE,利用AAS得到三角形PAF与三角形PAE全等,利用全等三角形对应边相等得到PE=PF,利用HL得到直角三角形PBE与直角三角形PCF全等,利用全等三角形对应边相等得到BE=CF,根据AB-AE=BE,CF=AF+AC,等量代换即可得证.
解答: 解:连接PA,PB,PC,
解:连接PA,PB,PC,
∵直径PD⊥BC,
∴PD平分BC,即PD垂直平分BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵∠PAF=∠PBC,∠PAE=∠PCB,
∴∠PAF=∠PAE,
在△APF和△APE中,
,
∴△APF≌△APE(AAS),
∴PE=PF,
在Rt△PBE与Rt△PCF中,
,
∴Rt△PBE≌与Rt△PCF(HL),
∴BE=FC,
∴AB-AE=AC+AF,
∴2AE=AB-AC,
∴AE=
(AB-AC).
 解:连接PA,PB,PC,
解:连接PA,PB,PC,∵直径PD⊥BC,
∴PD平分BC,即PD垂直平分BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵∠PAF=∠PBC,∠PAE=∠PCB,
∴∠PAF=∠PAE,
在△APF和△APE中,
|
∴△APF≌△APE(AAS),
∴PE=PF,
在Rt△PBE与Rt△PCF中,
|
∴Rt△PBE≌与Rt△PCF(HL),
∴BE=FC,
∴AB-AE=AC+AF,
∴2AE=AB-AC,
∴AE=
| 1 |
| 2 |
点评:此题考查了全等三角形的判定与性质,圆周角定理,垂径定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列方程中,不是一元二次方程的是( )
| A、x2-4=0 | ||
B、x2+
| ||
| C、x2+2x+1=0 | ||
D、3x2+
|
若代数式3a4b2x与0.2a4b3x-1是同类项,则x的值是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |