题目内容
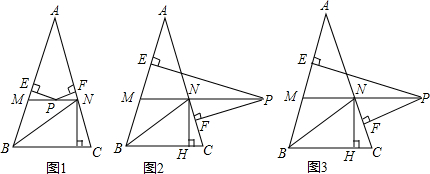
 如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF=( )
如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF=( )| A、60° | B、30° |
| C、60° | D、75° |
考点:等腰三角形的性质
专题:
分析:根据已知条件,利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算.
解答:解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°-(∠CBD+∠BDC)=180°-60°=120°,
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°,
∴∠CDE=180°-(∠ECD+∠CED)=180°-90°=90°,
∴∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°,
∴∠MEF=∠EFD+∠A=60°+15°=75°.
故选D.
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°-(∠CBD+∠BDC)=180°-60°=120°,
∴∠ECD=∠CED=180°-∠BCD-∠BCA=180°-120°-15°=45°,
∴∠CDE=180°-(∠ECD+∠CED)=180°-90°=90°,
∴∠EDF=∠EFD=180°-∠CDE-∠BDC=180°-90°-30°=60°,
∴∠MEF=∠EFD+∠A=60°+15°=75°.
故选D.
点评:本题主要考查了等腰三角形的性质及三角形内角和外角之间的关系.
(1)三角形的外角等于与它不相邻的两个内角和;
(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
(1)三角形的外角等于与它不相邻的两个内角和;
(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
把二次函数y=x2-4的图象向上平移3个单位,所得函数解析式为( )
| A、y=x2-7 |
| B、y=(x+3)2 |
| C、y=(x-3)2-4 |
| D、y=x2-1 |
下列方程中,不是一元二次方程的是( )
| A、x2-4=0 | ||
B、x2+
| ||
| C、x2+2x+1=0 | ||
D、3x2+
|
 如图,数a,b在数轴上对应位置是A、B,则-a,-b,a,b的大小关系是( )
如图,数a,b在数轴上对应位置是A、B,则-a,-b,a,b的大小关系是( )| A、-a<-b<a<b |
| B、a<-b<-a<b |
| C、-b<a<-a<b |
| D、以上都不对 |
由于b的取值不同,直线y=2x+b与曲线y=|x2-4x+3|的交点( )
| A、最多4个 |
| B、可能是3个 |
| C、可能是0,1,2个 |
| D、可能是0,1,2,4个 |
若A=10a2+2b2-7a+6,B=a2+2b2+5a-1,则A-B的值是( )
| A、正数 | B、负数 | C、0 | D、可正可负 |
若代数式3a4b2x与0.2a4b3x-1是同类项,则x的值是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、0 |