题目内容
已知二次函数的图象满足下列条件,求它的函数表达式:
(1)经过原点和点(-1,3),对称轴为直线x=4;
(2)经过点(1,1),(-2,1)和(2,3).
(1)经过原点和点(-1,3),对称轴为直线x=4;
(2)经过点(1,1),(-2,1)和(2,3).
考点:待定系数法求二次函数解析式
专题:计算题
分析:(1)先利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为((8,0),则可设交点式y=ax(x-8),然后把(-1,3)代入求出a即可;
(2)设一般式y=ax2+bx+c,然后把三个点的坐标代入得到关于a、b、c的方程组,再解方程组即可.
(2)设一般式y=ax2+bx+c,然后把三个点的坐标代入得到关于a、b、c的方程组,再解方程组即可.
解答:解:(1)∵抛物线的对称轴为直线x=4,
∴抛物线与x轴的另一个交点坐标为((8,0),
设抛物线解析式为y=ax(x-8),
把(-1,3)代入得a×(-1)(-1-8)=3,解得a=
,
∴抛物线解析式为y=
x(x-8)=
x2-
x;
(2)设抛物线解析式为y=ax2+bx+c,
根据题意
,解得
,
所以抛物线解析式为y=
x2+
x.
∴抛物线与x轴的另一个交点坐标为((8,0),
设抛物线解析式为y=ax(x-8),
把(-1,3)代入得a×(-1)(-1-8)=3,解得a=
| 1 |
| 3 |
∴抛物线解析式为y=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
(2)设抛物线解析式为y=ax2+bx+c,
根据题意
|
|
所以抛物线解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
下列分式中是最简分式的是( )
A、
| ||
B、
| ||
C、-
| ||
D、
|
下列运算正确的是( )
| A、(-ab)2=a2b2 |
| B、2a+b=2ab |
| C、a2•a2=2a2 |
| D、a4+a2=2 |
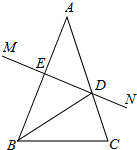 如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于点D,交AC于点M,以下结论不正确的是( )
如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于点D,交AC于点M,以下结论不正确的是( )| A、△BCD是等腰三角形 |
| B、线段BD是△ACB的角平分线 |
| C、△BCD的周长C△BCD=AB+BC |
| D、△ADM≌△BCD |
 △ABC中,D为BC边上任意一点,DE、DF分别是△ADB和△ADC的角平分线,连接EF,则△DEF的形状为
△ABC中,D为BC边上任意一点,DE、DF分别是△ADB和△ADC的角平分线,连接EF,则△DEF的形状为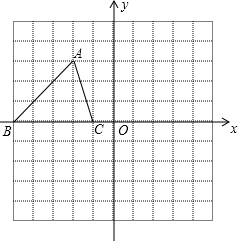 如图,已知A(-2,3)、B(-5,0)、C(-1,0),△ABC和△A1B1C1关于y轴对称.
如图,已知A(-2,3)、B(-5,0)、C(-1,0),△ABC和△A1B1C1关于y轴对称.