题目内容
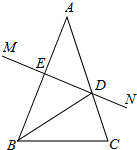如图，已知AB=AC，∠A=36°，AC的垂直平分线MN交AB于点D，交AC于点M，以下结论不正确的是（ ）| A、△BCD是等腰三角形 |
| B、线段BD是△ACB的角平分线 |
| C、△BCD的周长C△BCD=AB+BC |
| D、△ADM≌△BCD |
考点：线段垂直平分线的性质,等腰三角形的性质
专题：
分析：由AB=AC，∠A=36°，AC的垂直平分线MN交AB于点D，可得AD=BD，继而求得∠ABD=∠DBC=∠A=36°，∠BDC=∠C=72°，即可得△BCD是等腰三角形，△BCD的周长C△BCD=AB+BC，线段BD是△ACB的角平分线．
解答：解：∵AC的垂直平分线MN交AB于点D，
∴AD=BD，
∴∠ABD=∠A=36°，
∴AB=AC，
∴∠ABC=∠C=72°，
∴∠DBC=∠ABC-∠ABD=36°，
∴∠ABD=∠DBC，
即线段BD是△ACB的角平分线，故B正确；
∴∠BDC=72°，
∴∠BDC=∠C，
∴△BCD是等腰三角形，故A正确；
∴△BCD的周长C△BCD=BD+CD+BC=AD+CD+BC=AB+BC，故C正确；
∵△ADM是直角三角形，△BCD是顶角为36°的等腰三角形，故D错误．
故选D．
∴AD=BD，
∴∠ABD=∠A=36°，
∴AB=AC，
∴∠ABC=∠C=72°，
∴∠DBC=∠ABC-∠ABD=36°，
∴∠ABD=∠DBC，
即线段BD是△ACB的角平分线，故B正确；
∴∠BDC=72°，
∴∠BDC=∠C，
∴△BCD是等腰三角形，故A正确；
∴△BCD的周长C△BCD=BD+CD+BC=AD+CD+BC=AB+BC，故C正确；
∵△ADM是直角三角形，△BCD是顶角为36°的等腰三角形，故D错误．
故选D．
点评：此题考查了线段垂直平分线的性质以及等腰三角形的性质．此题难度不大，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
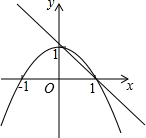如图，已知抛物线y1=-x2+1，直线y2=-x+1，当x任取一值时，x对应的函数值分别为y1，y2．若y1≠y2，取y1，y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=2时，y1=-3，y2=-1，y1＜y2，此时M=-3．下列判断中：
