题目内容
 △ABC中,D为BC边上任意一点,DE、DF分别是△ADB和△ADC的角平分线,连接EF,则△DEF的形状为
△ABC中,D为BC边上任意一点,DE、DF分别是△ADB和△ADC的角平分线,连接EF,则△DEF的形状为考点:直角三角形的性质,角平分线的定义
专题:
分析:根据角平分线的定义可得∠ADE=
∠ADB,∠ADF=
∠ADC,然后求出∠EDF=90°,再根据直角三角形的定义判断即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵DE、DF分别是△ADB和△ADC的角平分线,
∴∠ADE=
∠ADB,∠ADF=
∠ADC,
∴∠EDF=∠ADE+∠ADF=
∠ADB+
∠ADC=90°,
∴△DEF是直角三角形.
故答案为:直角三角形.
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EDF=∠ADE+∠ADF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△DEF是直角三角形.
故答案为:直角三角形.
点评:本题考查了直角三角形的性质,角平分线的定义,熟记概念并求出∠EDF=90°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在下列各式中,是关于x的分式方程的是( )
| A、2x-3y=0 | ||||
B、
| ||||
C、
| ||||
D、
|
下列说法错误的是( )
| A、两个等边三角形一定相似 |
| B、两个正方形一定相似 |
| C、两个菱形一定相似 |
| D、两个全等三角形一定相似 |
在等腰三角形、线段、平行四边形、五边形、和矩形,五种图形中一定是轴对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列三线段长,不能构成三角形的是( )
| A、2,3,4 |
| B、2,4,4 |
| C、2,4,6 |
| D、7,8,13 |
 点A、B、C在圆O上,AD⊥BC于点D,AP平分∠BAC,求证:∠OAP=∠PAD.
点A、B、C在圆O上,AD⊥BC于点D,AP平分∠BAC,求证:∠OAP=∠PAD.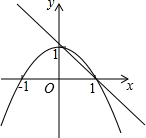 如图,已知抛物线y1=-x2+1,直线y2=-x+1,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=2时,y1=-3,y2=-1,y1<y2,此时M=-3.下列判断中:
如图,已知抛物线y1=-x2+1,直线y2=-x+1,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=2时,y1=-3,y2=-1,y1<y2,此时M=-3.下列判断中: