题目内容
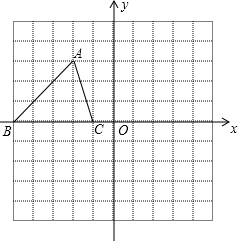 如图,已知A(-2,3)、B(-5,0)、C(-1,0),△ABC和△A1B1C1关于y轴对称.
如图,已知A(-2,3)、B(-5,0)、C(-1,0),△ABC和△A1B1C1关于y轴对称.(1)写出点A1、B1的坐标A1
(2)S△A1B1C1=
(3)若△DBC与△ABC全等,点D的坐标为
考点:全等三角形的性质,三角形的面积,关于x轴、y轴对称的点的坐标
专题:
分析:(1)根据关于y轴对称其纵坐标相等,横坐标变为相反数可求得A1、B1的坐标;
(2)可先求得△ABC的面积,由对称可得S△A1B1C1=S△ABC,可求得答案;
(3)由条件可知D到BC的距离和A到BC的距离相等,再结合全等可求得D点的坐标.
(2)可先求得△ABC的面积,由对称可得S△A1B1C1=S△ABC,可求得答案;
(3)由条件可知D到BC的距离和A到BC的距离相等,再结合全等可求得D点的坐标.
解答:解:
(1)∵A(-2,3)、B(-5,0)、C(-1,0),△ABC和△A1B1C1关于y轴对称,
∴A1坐标为(2,3)、B1坐标为(5,0),
故答案为:(2,3);(5,0);
(2)∵A(-2,3)、B(-5,0)、C(-1,0),
∴BC=4,A到BC的距离为3,
∴S△ABC=
×4×3=6,
∵△ABC和△A1B1C1关于y轴对称,
∴S△A1B1C1=S△ABC=6,
故答案为:6;
(3)当△DBC与△ABC全等时,可知D到BC的距离和A到BC的距离相等,
当D在x轴上方时,若△ABC≌△DBC,则D与A重合,此时D点坐标为(-2,3);若△ABC≌△DCB,则可知D点坐标为(-4,3);
当D在x轴下方时,同理可求得D点坐标为(-2,-3)或(-4,-3),
故答案为:(-2,3)或(-4,3)或(-2,-3)或(-4,-3).
(1)∵A(-2,3)、B(-5,0)、C(-1,0),△ABC和△A1B1C1关于y轴对称,
∴A1坐标为(2,3)、B1坐标为(5,0),
故答案为:(2,3);(5,0);
(2)∵A(-2,3)、B(-5,0)、C(-1,0),
∴BC=4,A到BC的距离为3,
∴S△ABC=
| 1 |
| 2 |
∵△ABC和△A1B1C1关于y轴对称,
∴S△A1B1C1=S△ABC=6,
故答案为:6;
(3)当△DBC与△ABC全等时,可知D到BC的距离和A到BC的距离相等,
当D在x轴上方时,若△ABC≌△DBC,则D与A重合,此时D点坐标为(-2,3);若△ABC≌△DCB,则可知D点坐标为(-4,3);
当D在x轴下方时,同理可求得D点坐标为(-2,-3)或(-4,-3),
故答案为:(-2,3)或(-4,3)或(-2,-3)或(-4,-3).
点评:本题主要考查关于y轴对称的点的坐标特征及全等三角形的性质,掌握关于y轴对称的点的纵坐标相等、横坐标互为相反数是解题的关键.

练习册系列答案
相关题目
在等腰三角形、线段、平行四边形、五边形、和矩形,五种图形中一定是轴对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列多项式中,能用平方差公式进行因式分解的是( )
| A、-64+m2 |
| B、-64-m2 |
| C、64+(-m)2 |
| D、64+m2 |
 如图,已知△ABC,
如图,已知△ABC,