题目内容
17．
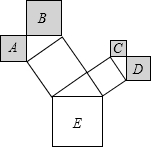如图是一株美丽的勾股树，所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的边长分别是3、4、2、3，则最大正方形E的面积是38．
分析 分别设中间两个正方形和最大正方形的边长为x，y，z，由勾股定理得出x2=32+52，y2=22+32，z2=x2+y2，即最大正方形的面积为：z2．
解答 解：设中间两个正方形的边长分别为x、y，最大正方形E的边长为z，则由勾股定理得：
x2=32+42=25；
y2=22+32=13；
z2=x2+y2=38；
即最大正方形E的面积=z2=38．
故答案为：38．
点评 本题考查了勾股定理、正方形的性质；采用了设“中间变量法”，分别由勾股定理求出x2，y2，再由勾股定理求出大正方形边长的平方z2=x2+y2是解决问题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如图，△ABE和△ADC是△ABC分别沿着AB，AC边翻折180°形成的，若∠1：∠2：∠3=10：5：3，则∠α的度数为160°．