题目内容
初中我们已经学过一次函数y=kx+b与反比例函数y=
(k≠0),它们具有哪些性质呢?请归纳总结.以函数y=x+
为例从以下几个方面研究函数y=x+
(k>0)的性质:
(1)你有几种画出该函数图象的方法;
(2)函数自变量x的取值范围;
(3)函数值y的取值范围;
(4)何时y随x的增加而增加?何时y随x的增加而减小?
(5)函数图象具有对称性吗?
(6)当x>0时函数有最小、最大值吗?
利用已有的性质,求下列函数值的取值范围:
①y=x+
(8≤x≤16)
②y=
+
(0<x≤1)
③y=
.
| k |
| x |
| 4 |
| x |
| k |
| x |
(1)你有几种画出该函数图象的方法;
(2)函数自变量x的取值范围;
(3)函数值y的取值范围;
(4)何时y随x的增加而增加?何时y随x的增加而减小?
(5)函数图象具有对称性吗?
(6)当x>0时函数有最小、最大值吗?
利用已有的性质,求下列函数值的取值范围:
①y=x+
| 16 |
| x |
②y=
| x |
| 2 |
| 2 |
| x |
③y=
| x2+5 | ||
|
考点:反比例函数综合题
专题:
分析:利用描点法画出函数图象,数形结合分析函数性质,逐步得出结论.
解答: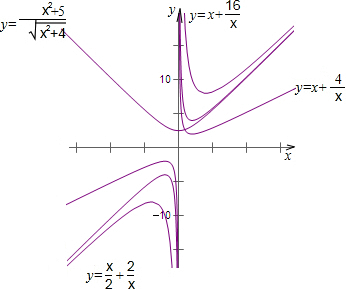 解:(1)描点法画函数图象;
解:(1)描点法画函数图象;
(2)对于y=x+
,x的取值范围是x≠0;
(3)∵x+
≥2
,
∴x+
≥4,
∴y≥4或y≤-4;
(4)根据(3),x>0时,当x=2时,函数取得最小值4;
x<0时,当x=-2时,函数取得最大值-4;
于是,x>2时,y随x的增加而增加;0<x<2时y随x的增加而减小;
x<-2时,y随x的增加而增加;-2<x<0时y随x的增加而减小.
(5)关于原点中心对称.
(6)当x=0时,函数有最小值4.
①当x=8时取得最小值10,当x=16时取得最大值17,故10≤x≤16;
②当x=1时取得最小值
,故y≥
;
③当x=0时取得最小值
,故y≥
.
 解:(1)描点法画函数图象;
解:(1)描点法画函数图象;(2)对于y=x+
| 4 |
| x |
(3)∵x+
| 4 |
| x |
x•
|
∴x+
| 4 |
| x |
∴y≥4或y≤-4;
(4)根据(3),x>0时,当x=2时,函数取得最小值4;
x<0时,当x=-2时,函数取得最大值-4;
于是,x>2时,y随x的增加而增加;0<x<2时y随x的增加而减小;
x<-2时,y随x的增加而增加;-2<x<0时y随x的增加而减小.
(5)关于原点中心对称.
(6)当x=0时,函数有最小值4.
①当x=8时取得最小值10,当x=16时取得最大值17,故10≤x≤16;
②当x=1时取得最小值
| 5 |
| 2 |
| 5 |
| 2 |
③当x=0时取得最小值
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题考查了反比例函数综合题,注意利用数形结合得出结论,要大胆探究,用描点法画出函数图象是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
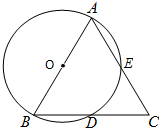 如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.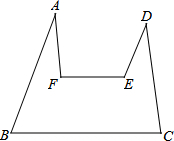 如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.
如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.