题目内容
将点A(3，2)沿x轴向左平移4个单位长度得到点A′，则点A′关于原点对称的点的坐标是( )
A. (-3，2) B. (-1，2) C. (1，2) D. (1，-2)
D
【解析】试题分析：将点A（3，2）向左平移4个单位长度得点A′，可得点A′的坐标为（﹣1，2），所以点A′关于y轴对称的点的坐标是（1，2），故选D．
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案已知二次函数y=﹣2x2+4x﹣3，如果y随x的增大而减小，那么x的取值范围是（ ）
A. x≥1 B. x≥0 C. x≥﹣1 D. x≥﹣2
A
【解析】【解析】
∵y=﹣2x2+4x﹣3=﹣2（x﹣1）2﹣1，∴抛物线开口向下，对称轴为x=1，∴当x≥1时，y随x的增大而减小．故选A． 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边)，设AB＝xm.
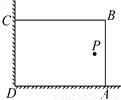
(1)若花园的面积为192m2，求x的值；
(2)若在P处有一棵树与墙CD、AD的距离分别是13m和6m，要将这棵树围在花园内(含边界，不考虑树的粗细)，求花园面积S的最大值．
(1)12或16(2)当x＝13时，S最大＝195
【解析】试题分析：（1）根据题意得出长×宽=192，进而得出答案；
（2）由在P处有一棵树与墙CD，AD的距离分别是13m和6m，求出x的取值范围，根据二次的性质求解即可.
试题解析：(1)(28－x)x＝192，解得x1＝12，x2＝16，
∴x的值为12或16.
(2)∵S＝x(28－x)＝－x2＋28x(6≤x≤1... 如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段AB',则点B'的坐标为_____.
(4,2)
【解析】试题分析：画出旋转后的图形位置，根据图形求解．
试题解析：AB旋转后位置如图所示．
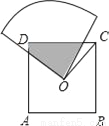
B′（4，2）． 如图，O是边长为a的正方形ABCD的中心，将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处，并将纸板的圆心绕O旋转，则正方形ABCD被纸板覆盖部分的面积为（ ）
A. 
a2 B. 
a2 C. 
a2 D. 
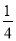a
B
【解析】【解析】
扇形的半径交AD于E，交CD于F，连结OD，如图．
∵四边形ABCD为正方形，∴OD=OC，∠COD=90°，∠ODA=∠OCD=45°．
∵∠EOF=90°，即∠EOD+∠DOF=90°，∠DOF+∠COF=90°，∴∠EOD=∠FOC．
在△ODE和△OCF中，∵∠ODE=∠OCF，OD=OC，∠EOD=∠COF，∴△ODE≌△OCF，∴S△OD... 如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=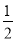
x刻画．
（1）请用配方法求二次函数图象的最高点P的坐标；
（2）小球的落点是A，求点A的坐标；
（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；
（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．
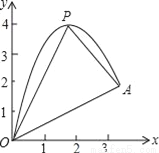
（1）最高点P的坐标为（2，4）；（2）点A的坐标为（， ）；（3）；（4）点M的坐标为（， ）
【解析】试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；
（2）联立两解析式，可求出交点A的坐标；
（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；
（4）过P... 如图，二次函数y=ax2﹣4x+c的图象经过坐标原点，与x轴交于点A（﹣4，0）．
（1）求二次函数的解析式；
（2）在抛物线上存在点P，满足S△AOP=8，请直接写出点P的坐标．
（1）y＝－－4x P1（－2， 4），P2（－2＋2，－4），P3（－2－2，－4）
【解析】试题分析：（1）把点A原点的坐标代入函数解析式，利用待定系数法求二次函数解析式解答；
（2）根据三角形的面积公式求出点P到AO的距离，然后分点P在x轴的上方与下方两种情况解答即可．
试题解析：（1）由已知条件得，
解得，
所以，此二次函数的解析式为y=﹣x2﹣4x；
... 已知在△ABC中，AB=AC。
（1）若D为AC的中点，BD把三角形的周长分为24cm和30cm两部分，求△ABC三边的长；
（2）若D为AC上一点，试说明AC＞
（BD+DC）。
（1）三角形的三边长为16，16，22或20，20，14；（2）理由见解析
【解析】试题分析：（1）分两种情况讨论：当AB+AD=30，BC+DC=24或AB+AD=24，BC+DC=30，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为16，16，22或20，20，14；
（2）根据三角形两边之和大于第三边即可得到AC＞（BD+DC）.
试题解析：
（1）设三角形... 分解因式：4x2－9y2.
(2x＋3y)(2x－3y)
【解析】试题分析：直接利用平方差公式因式分解即可.
试题解析：
4x2－9y2=(2x＋3y)(2x－3y).