题目内容
三角形内有一点，它到三边的距离相等，则这点是该三角形的( )
A. 三条中线交点 B. 三条角平分线交点
C. 三条高线交点 D. 三条高线所在直线交点
B
【解析】根据三角形角平分线上的点到角的两边的距离相等可得此点为角平分线的交点.
故选：B.
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段AB',则点B'的坐标为_____.
(4,2)
【解析】试题分析：画出旋转后的图形位置，根据图形求解．
试题解析：AB旋转后位置如图所示．
B′（4，2）． 已知在△ABC中，AB=AC。
（1）若D为AC的中点，BD把三角形的周长分为24cm和30cm两部分，求△ABC三边的长；
（2）若D为AC上一点，试说明AC＞
（BD+DC）。
（1）三角形的三边长为16，16，22或20，20，14；（2）理由见解析
【解析】试题分析：（1）分两种情况讨论：当AB+AD=30，BC+DC=24或AB+AD=24，BC+DC=30，所以根据等腰三角形的两腰相等和中线的性质可求得，三边长为16，16，22或20，20，14；
（2）根据三角形两边之和大于第三边即可得到AC＞（BD+DC）.
试题解析：
（1）设三角形... 已知：如图，△ABC中，BO，CO分别是∠ABC和∠ACB的平分线，过O点的直线分别交AB、AC于点D、E，且DE∥BC．若AB=6cm，AC=8cm，则△ADE的周长为__．
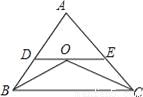
14cm
【解析】两直线平行，内错角相等，以及根据角平分线性质，可得△OBD、△EOC均为等腰三角形，由此把△AEF的周长转化为AC+AB．
【解析】
∵DE∥BC，∴∠DOB=∠OBC，又∵BO是∠ABC的角平分线，∴∠DBO=∠OBC，∴∠DBO=∠DOB，∴BD=OD，同理：OE=EC，
∴△ADE的周长=AD+OD+OE+EC=AD+BD+AE+EC=AB+AC=14c... 四条线段的长分别是5cm，6cm，8cm，13cm，以其中任意三条线段为边可以构成______个三角形．
2
【解析】首先发现每三条可以组合为5、6、8；5、6、13；5、8、13；6、8、13；
再根据三角形的三边关系，可知能构成三角形的为：5、6、8和6、8、13.
因此可构成2个三角形.
故答案为：2. 下列长度的各组线段中，能组成三角形的是 ( )
A. 4、5、6 B. 6、8、15 C. 5、7、12 D. 3、9、13
A
【解析】根据三角形的三边关系，得
A.4+5>6，能组成三角形，符合题意；
B.6+8<15，不能够组成三角形，不符合题意；
C.5+7=12，不能够组成三角形，不符合题意；
D.3+7<13，不能够组成三角形，不符合题意。
故选：A. 分解因式：4x2－9y2.
(2x＋3y)(2x－3y)
【解析】试题分析：直接利用平方差公式因式分解即可.
试题解析：
4x2－9y2=(2x＋3y)(2x－3y). 某工厂有一种产品现在的年产量是20万件，计划今后两年增加产量，如果每年都比上一年的产量增加x倍，那么两年后这种产品的产量y将随计划所定的x的值而确定，那么y与x之间的关系应表示为_____．
y=20(x+1)2
【解析】∵某工厂一种产品的年产量是20件，每一年都比上一年的产品增加x倍，
∴一年后产品是：20（1+x），
∴两年后产品y与x的函数关系是：y=20（1+x）2．
故答案为：y=20（x+1）2. 任取不等式组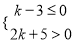
的一个整数解，则能使关于x的方程：2x＋k＝－1的解为非负数的可能性为____.
【解析】解不等式k-3≤0可得k≤3，解不等式2k+5＞0，可得k＞-，所以可求得不等式组的解集为-＜k≤3，所以k的整数解为-2、-1、0、1、2、3，分别代入方程2x+k=-1，可得x=、0、-、-1、-、-2，所以非负数解有了两个，其可能性为： .
故答案为： .