题目内容
15. 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE=BF,EF=BD,且AD:DB=3:5,那么CF:CB等于( )
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE=BF,EF=BD,且AD:DB=3:5,那么CF:CB等于( )| A. | 3:5 | B. | 3:8 | C. | 5:8 | D. | 2:5 |
分析 根据DE=BF,EF=BD,证明四边形BDEF是平行四边形,得到DE∥BF,EF∥BD,根据平行线分线段成比例定理得到答案.
解答 解:∵DE=BF,EF=BD,
∴四边形BDEF是平行四边形,
∴DE∥BF,EF∥BD,
∴$\frac{AE}{EC}$=$\frac{AD}{DB}$=$\frac{3}{5}$,
∴$\frac{CF}{FB}$=$\frac{CE}{EA}$=$\frac{5}{3}$,
则$\frac{CF}{CB}$=$\frac{5}{8}$.
故选:C.
点评 本题考查的是平行四边形的判定和性质以及平行线分线段成比例定理,掌握定理的应用是解题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
20.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
| A. | 32,31 | B. | 31,32 | C. | 31,31 | D. | 32,35 |
4.与方程组$\left\{\begin{array}{l}{x+3y=-3}\\{x+y=-2}\end{array}\right.$有相同解的方程组是( )
| A. | $\left\{\begin{array}{l}{x-y=1}\\{3x=5-y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y-1}\\{3x=5-y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-1}\\{3x+5+y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y-1}\\{3x+5-y=0}\end{array}\right.$ |
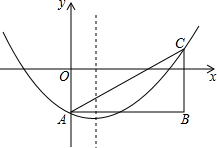 如图,在平面直角坐标系中,抛物线y=ax2-2ax-2(a>0)与y轴交于点A,点B的坐标为($\frac{1}{a}$,-2),过点B作y轴的平行线,交抛物线于点C,连结AB、AC.
如图,在平面直角坐标系中,抛物线y=ax2-2ax-2(a>0)与y轴交于点A,点B的坐标为($\frac{1}{a}$,-2),过点B作y轴的平行线,交抛物线于点C,连结AB、AC.