题目内容
2．某宾馆有50个房间供游客居住，当每个房间每天的房价为180元时房间全部住满，当每个房间每天的定价增加10元时，就会有一间房空闲，如果游客居住房间宾馆，需对每个房间每天支出20元的各种费用，设每个房间的房价每天增加x元．
（1）求一天订住的房间数y与x之间的函数关系式；
（2）求宾馆一天的利润w元与x之间的函数关系式；
（3）房间定价为多少元时，宾馆一天的利润最大？最大利润是多少？
分析 （1）设每个房间每天的定价增加x元，利用当每个房间每天的定价增加10元时，就会有一间房空闲进而得出y与x之间的函数关系式；
（2）设每个房间每天的定价增加x元，宾馆所得利润为W，利用租房利润减去各种费用，可得利润函数关系式；
（3）利用公式法直接求出二次函数最值即可．
解答 解：（1）设每个房间每天的定价增加x元，
则一天订住的房间数y与x之间的函数关系式为：y=50-$\frac{x}{10}$；
（2）设每个房间每天的定价增加x元，宾馆所得利润为：
w=（180+x-20）（50-$\frac{x}{10}$），
即w=-$\frac{1}{10}$x2+34x+8000；
（3）由题意可得：0≤x≤500，且x是10的倍数．
当x=-$\frac{b}{2a}$=170时，
∴房价定为180+170=350时，宾馆利润最大．
∴y最大=10890（元）．
答：房价定为350元，宾馆利润最大，一天的最大利润为10890元．
点评 本题考查了二次函数的应用，要求同学们仔细审题，将实际问题转化为数学模型，注意公式法求二次函数最值的应用．
练习册系列答案
相关题目
7．现从A、B向甲、乙两地运送蔬菜，A，B两个蔬菜市场各有蔬菜14吨，其中甲地需要蔬菜15吨，乙地需要蔬菜13吨，从A到甲地运费50元/吨，到乙地30元/吨；从B地到甲运费60元/吨，到乙地45元/吨．
（1）设A地到甲地运送蔬菜x吨，请完成下表：
（2）设总运费为W元，请写出W与x的函数关系式；
（3）怎样调运蔬菜才能使运费最少？并求出最少的运费值．
（1）设A地到甲地运送蔬菜x吨，请完成下表：
| 运往甲地（单位：吨） | 运往乙地（单位：吨） | |
| A | x | 14-x |
| B | 15-x | x-1 |
（3）怎样调运蔬菜才能使运费最少？并求出最少的运费值．
11．
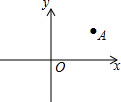如图，已知点A（2，3），将点A绕原点O顺时针旋转90°到A′，则点A′的坐标为（ ）
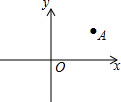如图，已知点A（2，3），将点A绕原点O顺时针旋转90°到A′，则点A′的坐标为（ ）| A． | （-2，3） | B． | （-3，2） | C． | （2，-3） | D． | （3，-2） |
