题目内容
11.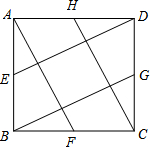 拿一张正方形纸片ABCD(如图),取它的四条边的中点E,F,G,H,连接AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的面积为5平方厘米,则正方形纸片ABCD的边长为5厘米.
拿一张正方形纸片ABCD(如图),取它的四条边的中点E,F,G,H,连接AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的面积为5平方厘米,则正方形纸片ABCD的边长为5厘米.
分析 根据题意可知小正方形的边长为$\sqrt{5}$,利用中位线的性质以及全等三角形的判定与性质即可求出正方形ABCD的边长.
解答 解: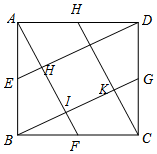 由题意可知:HI=IK=$\sqrt{5}$,
由题意可知:HI=IK=$\sqrt{5}$,
ED∥BG,
∵E是AB的中点,
∴EH是△ABI的中位线,
∴AH=HI=$\sqrt{5}$
∵∠BAI+∠ABI=∠ABI+∠CBK=90°,
∴∠BAI=∠CBK
在△ABI与△CBK中,
$\left\{\begin{array}{l}{∠BAI=∠CBK}\\{∠AIB=∠CKB}\\{AB=BC}\end{array}\right.$
∴△ABI≌△CBK(AAS)
∴BK=AI=2$\sqrt{5}$
同理可知:FI是△CBK的中位线,
∴BI=$\sqrt{5}$
由勾股定理可知:AB=5,
故答案为:5
点评 本题考查算术平方根,解题的关键是利用中位线的性质与全等三角形的性质与判定,本题属于中等题型.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
19.若m=32,n=43,则126的值(用舍m、n的式子表示)为( )
| A. | mn | B. | m2n2 | C. | m2n3 | D. | m3n2 |

 如图,二次函数y=ax2+bx+c的图象如图,则点P(a,-$\frac{c}{b}$)在第三象限.
如图,二次函数y=ax2+bx+c的图象如图,则点P(a,-$\frac{c}{b}$)在第三象限.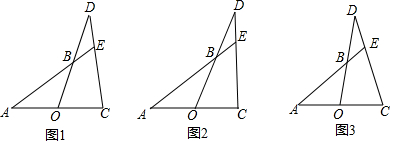
 如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=2$\sqrt{3}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值$\frac{3}{2}\sqrt{2}$.
如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=2$\sqrt{3}$,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值$\frac{3}{2}\sqrt{2}$.