题目内容

1．已知x=-2为方程x2+ax+2b=0的一根，则a2+b2的最小值为2．

分析 将x=-2代入原方程即可得出a=b+2，将a=b+2代入a2+b2中利用配方法将其变形为2（b+1）2+2，再根据偶次方程的非负性即可得出a2+b2的最小值．

解答 解：∵x=-2为方程x2+ax+2b=0的一根，
∴4-2a+2b=0，
∴a=b+2，
∴a2+b2=（b+2）2+b2=2b2+4b+4=2（b+1）2+2≥2．
故答案为：2．

点评 本题考查了配方法的应用、一元二次方程的解以及偶次方的非负性，根据一元二次方程的解找出a=b+2时解题的关键．

练习册系列答案
相关题目
11．下列命题中，①三角形三条高（或高的延长线）的交点不在三角形的内部，就在三角形的外部；②一个多边形的边数每增加一条，这个多边形的内角和就增加360°；③两条平行直线被第三条直线所截，同旁内角的角平分线互相平行；④三角形的一个外角等于任意两个内角的和；⑤一个三角形中至少有两个锐角；⑥在△ABC中，若∠A=2∠B=3∠C，则△ABC为直角三角形，其中假命题是（　　）
A．①②③④B．②④⑥C．②③⑤D．①②③④⑥
12．计算：$\frac{a}{a+b}$-$\frac{b}{a-b}$+$\frac{{b}^{2}}{{a}^{2}-{b}^{2}}$．
9．一个正多边形的每个内角都是150°，则它是正十二边形．
16．解下列方程：
（1）$\frac{0.1x-2}{0.3}$+$\frac{3-0.2x}{0.4}$=1                               
（2）$\frac{x-1}{2}$-$\frac{x-2}{4}$=$\frac{x}{3}$-1．
6．等腰三角形一腰上的高与另一腰的夹角为32°，则该等腰三角形的底角的度数为61°或29°．
13．阅读理解：在实数范围内，当a＞0且b＞0时，我们由非负数的性质知道（$\sqrt{a}$-$\sqrt{b}$）2≥0，所以a-2$\sqrt{ab}$+b≥0，即：a+b≥2$\sqrt{ab}$，当且仅当a=b时，等号成立，这就是数学上有名的“均值不等式”，若a与b的积为定值p（p＞0），则a+b有最小值2$\sqrt{p}$；若a与b的和为定值q（q＞0），则ab有最大值$\frac{{q}^{2}}{4}$，请根据上述内容，回答下列问题．
（1）若x＞0，则当x=2时，代数式2x+$\frac{8}{x}$取最小值8；
（2）已知：y1与x-2成正比例函数关系，y2与x+2成反比例函数关系，且y=y1+y2，当x=6时，y=9；当x=-1时，y=2，求当x＞-2时y的最小值．
10．一个正方形的面积扩大为原来的4倍，它的边长变为原来的多少倍？面积扩大为原来的9倍，它的边长变为原来的多少倍？面积扩大为原来的n倍，它的边长变为原来的多少倍？
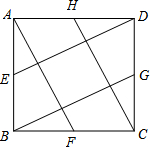11．拿一张正方形纸片ABCD（如图），取它的四条边的中点E，F，G，H，连接AF，BG，CH，DE．沿这些连线剪4刀，便剪出中间这个较小的正方形（阴影部分）．请试一试，若要剪出的小正方形的面积为5平方厘米，则正方形纸片ABCD的边长为5厘米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网