题目内容
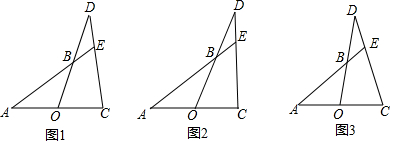
20.点C,D分别是△ABO的边AO、OB延长线上的点,AB的延长线交DC于E.(1)如图1,OA=OC,AB=CD,求证:DE=BE;
(2)如图2,OA=OC,∠C=90°,AC=CD,CE=3DE,求sin∠ABO;
(3)如图3,若BE=DE,$\frac{AO}{OC}$=$\frac{2}{3}$,AB=4,求DC的长.
分析 (1)如图1中,作CF∥AE交DO的延长线于F.由△AOB≌△COF,推出AB=CF,由AB=CD,推出CF=CD,推出∠D=∠F=∠ABO,即可解决问题.
(2)如图2中,作OF∥CD交AE于F,EH⊥OD于H.设DE=a.则EC=3a,AC=DC=4a,由OA=OC,FO∥EC,推出AF=EF,FO=$\frac{1}{2}$EC=$\frac{3a}{2}$,在Rt△AEC中,AE=$\sqrt{(4a)^{2}+(3a)^{2}}$=5a,推出AF=EF=$\frac{5}{2}a$,由OF∥DE,推出$\frac{BF}{BE}$=$\frac{OF}{DE}$=$\frac{\frac{3}{2}a}{a}$=$\frac{3}{2}$,推出BE=$\frac{2}{5}$EF=a,由∠D=∠D,∠EHD=∠C=90°,推出△DEH∽△DOC,推出$\frac{DE}{OD}$=$\frac{HE}{OC}$,推出$\frac{a}{2\sqrt{5}a}$=$\frac{HE}{2a}$,推出HE=$\frac{\sqrt{5}}{5}$a,根据sin∠ABO=sin∠HBE=$\frac{EH}{BE}$,计算即可.
(3)如图3中,作CF∥AB交DO于F.求出CF的长,只要证明CD=CF即可解决问题.
解答 解:(1)如图1中,作CF∥AE交DO的延长线于F.
∵CF∥AB,
∴∠A=∠FCO,∠ABO=∠F,
在△AOB和△COF中,
$\left\{\begin{array}{l}{∠A=∠OCF}\\{OA=OC}\\{∠AOB=∠COF}\end{array}\right.$,
∴△AOB≌△COF,
∴AB=CF,
∵AB=CD,
∴CF=CD,
∴∠D=∠F=∠ABO,
∵∠ABO=∠DBE,
∴∠D=∠DBE,
∴ED=EB.
(2)如图2中,作OF∥CD交AE于F,EH⊥OD于H.设DE=a.则EC=3a,AC=DC=4a,
∵OA=OC,FO∥EC,
∴AF=EF,FO=$\frac{1}{2}$EC=$\frac{3a}{2}$,
在Rt△AEC中,AE=$\sqrt{(4a)^{2}+(3a)^{2}}$=5a,
∴AF=EF=$\frac{5}{2}a$,
∵OF∥DE,
∴$\frac{BF}{BE}$=$\frac{OF}{DE}$=$\frac{\frac{3}{2}a}{a}$=$\frac{3}{2}$,
∴BE=$\frac{2}{5}$EF=a,
∵∠D=∠D,∠EHD=∠C=90°,
∴△DEH∽△DOC,
∴$\frac{DE}{OD}$=$\frac{HE}{OC}$,
∴$\frac{a}{2\sqrt{5}a}$=$\frac{HE}{2a}$,
∴HE=$\frac{\sqrt{5}}{5}$a,
∴sin∠ABO=sin∠HBE=$\frac{EH}{BE}$=$\frac{\frac{\sqrt{5}}{5}a}{a}$=$\frac{\sqrt{5}}{5}$.
(3)如图3中,作CF∥AB交DO于F.
∵AB∥CF,
∴$\frac{AB}{CF}$=$\frac{OA}{OC}$=$\frac{2}{3}$,
∵AB=4,
∴CF=6,
∵EB=ED,
∴∠D=∠DBE=∠ABO,
∵∠ABO=∠F,
∴∠D=∠F,
∴CD=CF=6.
点评 本题考查相似三角形综合题、等腰三角形的判定和性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | a=6,b=8,c=10 | B. | a=5k,b=12k,c=13k | ||
| C. | a=5,b=7,c=8 | D. | a=$\sqrt{7}$,b=$\sqrt{3}$,c=2 |
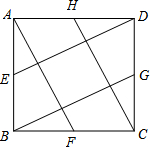 拿一张正方形纸片ABCD(如图),取它的四条边的中点E,F,G,H,连接AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的面积为5平方厘米,则正方形纸片ABCD的边长为5厘米.
拿一张正方形纸片ABCD(如图),取它的四条边的中点E,F,G,H,连接AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的面积为5平方厘米,则正方形纸片ABCD的边长为5厘米.