题目内容
16．
如图，二次函数y=ax2+bx+c的图象如图，则点P（a，-$\frac{c}{b}$）在第三象限．
分析 根据开口方向得出a的符号，根据抛物线与y轴的交点得出c的符号，再由对称轴得出b的符号，根据各个象限内点的坐标特征即可得出答案．
解答 解：∵抛物线开口向下，
∴a＜0，
∵抛物线与y轴的正半轴相交，
∴c＞0，
∵-$\frac{b}{2a}$＞0，
∴b＞0，
∴P（a，-$\frac{c}{b}$）在第三象限，
故答案为三．
点评 本题考查了二次函数的图象与系数的关系，掌握开口方向，抛物线与y轴的交点，对称轴以及各个象限内点的坐标特征是解题的关键．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
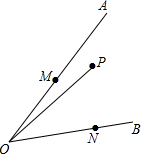如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运运，若∠AOB=45°，OP=2$\sqrt{2}$，则△PMN的周长的最小值为4．
4．下列式子正确的是（ ）
| A． | x-（y-z）=x-y-z | B． | -（x-y+z）=-x-y+z | ||
| C． | x+2y+2z=x-2（y+z） | D． | -a+c+d-b=-（a+b）+（c+d） |
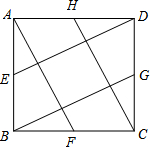拿一张正方形纸片ABCD（如图），取它的四条边的中点E，F，G，H，连接AF，BG，CH，DE．沿这些连线剪4刀，便剪出中间这个较小的正方形（阴影部分）．请试一试，若要剪出的小正方形的面积为5平方厘米，则正方形纸片ABCD的边长为5厘米．
5．根据下列条件分别判别以a，b，c为边的三角形不是直角三角形的是（ ）
| A． | a=6，b=8，c=10 | B． | a=5k，b=12k，c=13k | ||
| C． | a=5，b=7，c=8 | D． | a=$\sqrt{7}$，b=$\sqrt{3}$，c=2 |