题目内容
4．甲、乙两人进行射击测试，每人10次射击成绩平均是均为9.2环，方差分别为S甲2、S乙2，若甲的成绩更稳定，则S甲2、S乙2的大小关系为（ ）| A． | S甲2＞S乙2 | B． | S甲2＜S乙2 | C． | S甲2=S乙2 | D． | 无法确定 |
分析 根据方差的性质进行判断即可．
解答 解：∵每人10次射击成绩平均是均为9.2环，甲的成绩更稳定，
∴S甲2＜S乙2，
故选：B．
点评 本题考查的是方差的性质，掌握方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立是解题的关键．
练习册系列答案
口算能手系列答案
相关题目
14．
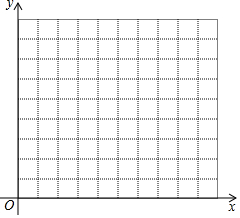已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如表所示．
（1）观察表中各对应点坐标的变化，并填空：a=0，b=2，c=9；
（2）在如图所示直角坐标系中画出△ABC和△A′B′C′；
（3）连CC′、BB′，直接写出CC′与BB′的数量关系和位置关系：平行且相等．
已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如表所示．| △ABC | A（a，0） | B（4，0） | C（5，5） |
| △A′B′C′ | A′（4，2） | B′（8，b） | C′（c，7） |
（2）在如图所示直角坐标系中画出△ABC和△A′B′C′；
（3）连CC′、BB′，直接写出CC′与BB′的数量关系和位置关系：平行且相等．
15．
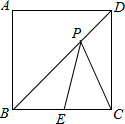如图，正方形ABCD的边长为3，E是BC中点，P为BD上一动点，则PE+PC的最小值为（ ）
如图，正方形ABCD的边长为3，E是BC中点，P为BD上一动点，则PE+PC的最小值为（ ）| A． | $\frac{2}{3}$$\sqrt{5}$ | B． | 2$\sqrt{3}$ | C． | $\frac{3}{2}$$\sqrt{5}$ | D． | 2 |
如图，∠1=30°，则∠A+∠B+∠C+∠D+∠E+∠F=300度．
9．
如图，在点M，N，P，Q中，一次函数y=kx+2（k＜0）的图象不可能经过的点是（ ）
如图，在点M，N，P，Q中，一次函数y=kx+2（k＜0）的图象不可能经过的点是（ ）| A． | M | B． | N | C． | P | D． | Q |
13．下列计算正确的是（ ）
| A． | -5+2=-7 | B． | 6÷（-2）=-3 | C． | （-1）2017=1 | D． | -20=1 |
14．下列各式中，是最简二次根式的是（ ）
| A． | $\sqrt{{m}^{2}+1}$ | B． | $\sqrt{\frac{a}{5}}$ | C． | $\sqrt{27}$ | D． | $\sqrt{5{a}^{2}b}$ |