题目内容
15.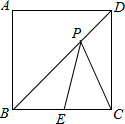 如图,正方形ABCD的边长为3,E是BC中点,P为BD上一动点,则PE+PC的最小值为( )
如图,正方形ABCD的边长为3,E是BC中点,P为BD上一动点,则PE+PC的最小值为( )| A. | $\frac{2}{3}$$\sqrt{5}$ | B. | 2$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{5}$ | D. | 2 |
分析 要求PE+PC的最小值,PE,PC不能直接求,可考虑通过作辅助线转化PE,PC的值,从而找出其最小值求解.
解答 解:如图,连接AE,
∵点C关于BD的对称点为点A,
∴PE+PC=PE+AP,
根据两点之间线段最短可得AE就是AP+PE的最小值,
∵正方形ABCD的边长为2,E是BC边的中点,
∴BE=1.5,
∴AE=$\sqrt{{3}^{2}+1.{5}^{2}}$=$\frac{3}{2}$$\sqrt{5}$,
故选C.
点评 此题主要考查了正方形的性质和轴对称及勾股定理等知识的综合应用.根据已知得出两点之间线段最短可得AE就是AP+PE的最小值是解题关键.

练习册系列答案
相关题目
5.已知m<0,关于x的方程(x-2)2-m=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有两个实数根 |
6.若一次函数y=(k-3)x-k的图象经过第二、三、四象限,则k的取值范围是( )
| A. | k<3 | B. | k<0 | C. | k>3 | D. | 0<k<3 |
10.若分式$\frac{2x-1}{x+3}$的值为0,则x的值为( )
| A. | -$\frac{1}{2}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | x≠-3 |
4.甲、乙两人进行射击测试,每人10次射击成绩平均是均为9.2环,方差分别为S甲2、S乙2,若甲的成绩更稳定,则S甲2、S乙2的大小关系为( )
| A. | S甲2>S乙2 | B. | S甲2<S乙2 | C. | S甲2=S乙2 | D. | 无法确定 |
5.若多项式(x+1)(x-3)=x2+ax+b,则a,b的值分别是( )
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
 如图△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,AE=3,则点B到ED的距离是4.
如图△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,AE=3,则点B到ED的距离是4.