题目内容
17.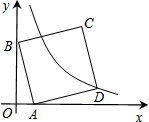 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上则a的值是( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上则a的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F,易证△OAB≌△FDA≌△BEC,求得A、B的坐标,根据全等三角形的性质可以求得C、D的坐标,从而利用待定系数法求得反比例函数的解析式,进而求得G的坐标,则a的值即可求解.
解答 解:作CE⊥y轴于点E,交双曲线于点G.作DF⊥x轴于点F.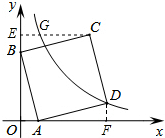
在y=-3x+3中,令x=0,解得:y=3,即B的坐标是(0,3).
令y=0,解得:x=1,即A的坐标是(1,0).
则OB=3,OA=1.
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
又∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,
$\left\{\begin{array}{l}{∠DAF=∠OBA}\\{∠BOA=∠AFD}\\{AD=AD}\end{array}\right.$,
∴△OAB≌△FDA(AAS),
同理,△OAB≌△FDA≌△BEC,
∴AF=OB=EC=3,DF=OA=BE=1,
故D的坐标是(4,1),C的坐标是(3,4).代入y=$\frac{k}{x}$得:k=4,则函数的解析式是:y=$\frac{4}{x}$.
∴OE=4,
则C的纵坐标是4,把y=4代入y=$\frac{4}{x}$得:x=1.即G的坐标是(1,4),
∴CG=2,
∴a=2.
故选B.
点评 本题考查了正方形的性质,反比例函数图象上点的坐标特征,全等三角形的判定与性质,待定系数法求函数的解析式,正确求得C、D的坐标是关键.

练习册系列答案
相关题目
5.在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
| A. | 1 | B. | 1或$\frac{\sqrt{3}-1}{2}$ | C. | 1或$\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$ |
12.下列运算中,正确的是( )
| A. | x2+x4=x6 | B. | (-x3)2=x6 | C. | 2a+3b=5ab | D. | x6÷x3=x2(x≠0) |
2.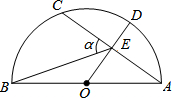 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )| A. | $\frac{3\sqrt{13}}{13}$ | B. | $\frac{2\sqrt{13}}{13}$ | C. | $\frac{\sqrt{13}}{13}$ | D. | $\frac{2}{3}$ |
7.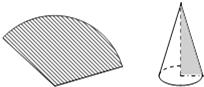 用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
 用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )| A. | 2cm | B. | 3$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
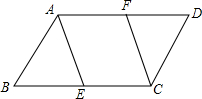 如图,在?ABCD中,点E、F分别是BC、AD的中点
如图,在?ABCD中,点E、F分别是BC、AD的中点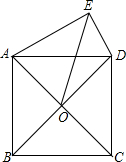 如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE=4$\sqrt{2}$,则AE=5.
如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE=4$\sqrt{2}$,则AE=5.