题目内容
18.计算(1)(2$\sqrt{3}$+$\sqrt{2}$)(2$\sqrt{3}$-$\sqrt{2}$);
( 2)$\frac{2}{\sqrt{3}+1}$+$\frac{\sqrt{3}}{2}$+1;
(3)3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$;
(4)($\frac{3}{4}$$\sqrt{15}$-$\sqrt{12}$)÷$\frac{\sqrt{3}}{2}$.
分析 (1)直接利用平方差公式计算求出答案;
(2)首先化简二次根式,进而合并求出答案;
(3)首先化简二次根式,进而合并求出答案;
(4)直接化简二次根式,进而利用二次根式除法运算法则答案.
解答 解:(1)(2$\sqrt{3}$+$\sqrt{2}$)(2$\sqrt{3}$-$\sqrt{2}$)
=(2$\sqrt{3}$)2-($\sqrt{2}$)2
=12-2
=10;
( 2)$\frac{2}{\sqrt{3}+1}$+$\frac{\sqrt{3}}{2}$+1
=$\frac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$+$\frac{\sqrt{3}}{2}$+1
=$\sqrt{3}$-1+$\frac{\sqrt{3}}{2}$+1
=$\frac{3\sqrt{3}}{2}$;
(3)3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$
=9$\sqrt{2}$+$\frac{1}{5}$×5$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$
=10$\sqrt{2}$-2$\sqrt{2}$
=8$\sqrt{2}$;
(4)($\frac{3}{4}$$\sqrt{15}$-$\sqrt{12}$)÷$\frac{\sqrt{3}}{2}$
=$\frac{3}{4}$$\sqrt{15}$×$\frac{2}{\sqrt{3}}$-2$\sqrt{3}$×$\frac{2}{\sqrt{3}}$
=$\frac{3}{2}$$\sqrt{5}$-4.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
3.当x=-2时,代数式x+1的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
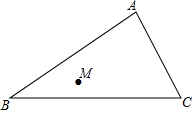 已知△ABC及点M,试画出△A1B1C1和△A2B2C2,使△A1B1C1和△ABC关于点M成中心对称,使△A2B2C2和△ABC关于AC所在直线成轴对称.
已知△ABC及点M,试画出△A1B1C1和△A2B2C2,使△A1B1C1和△ABC关于点M成中心对称,使△A2B2C2和△ABC关于AC所在直线成轴对称.
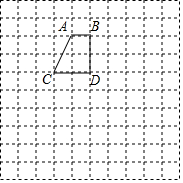 在如图中的正方形网格中有一个直角梯形ABCD,请你在图中分别按下列要求画出图形(不要求写出画法)
在如图中的正方形网格中有一个直角梯形ABCD,请你在图中分别按下列要求画出图形(不要求写出画法)