题目内容
4.若|a-1|+|b+3|=0,则a-b=4.分析 根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.
解答 解:∵|a-1|+|b+3|=0,
∴a-1=0,b+3=0,
∴a=1,b=-3,
∴a-b=4,
故答案为:4.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.梯形上底为a,下底为b,高为(2a-b),则梯形的面积是( )
| A. | ${a^2}+\frac{1}{2}ab-\frac{1}{2}{b^2}$ | B. | 2a2+ab-b2 | C. | ${a^2}-\frac{1}{2}{b^2}$ | D. | ${a^2}+ab-\frac{1}{2}{b^2}$ |
13.若0是一元二次方程(m-1)x2+6x+m2-1=0的一个根,则m取值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 以上都不是 |
14.八边形的对角线共有( )
| A. | 8条 | B. | 16条 | C. | 18条 | D. | 20条 |
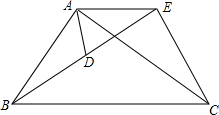 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.