题目内容
12.梯形上底为a,下底为b,高为(2a-b),则梯形的面积是( )| A. | ${a^2}+\frac{1}{2}ab-\frac{1}{2}{b^2}$ | B. | 2a2+ab-b2 | C. | ${a^2}-\frac{1}{2}{b^2}$ | D. | ${a^2}+ab-\frac{1}{2}{b^2}$ |
分析 利用梯形的面积公式列出关系式,利用多项式乘以多项式法则计算即可得到结果.
解答 解:根据题意得:S=$\frac{1}{2}$(a+b)(2a-b)=a2+$\frac{1}{2}$ab-$\frac{1}{2}$b2.
故选A
点评 此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
2.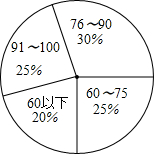 某校对七年级的300名学生数学考试做一次调查,在某范围内的得分情况如图所示的扇形图,则在75分以下这一分数段中的人数为( )
某校对七年级的300名学生数学考试做一次调查,在某范围内的得分情况如图所示的扇形图,则在75分以下这一分数段中的人数为( )
 某校对七年级的300名学生数学考试做一次调查,在某范围内的得分情况如图所示的扇形图,则在75分以下这一分数段中的人数为( )
某校对七年级的300名学生数学考试做一次调查,在某范围内的得分情况如图所示的扇形图,则在75分以下这一分数段中的人数为( )| A. | 75人 | B. | 125人 | C. | 135人 | D. | 165人 |
1. 有理数a,b,c在数轴上大致位置如图,则下列关系式正确的是( )
有理数a,b,c在数轴上大致位置如图,则下列关系式正确的是( )
 有理数a,b,c在数轴上大致位置如图,则下列关系式正确的是( )
有理数a,b,c在数轴上大致位置如图,则下列关系式正确的是( )| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | |a|<|b|<|c| |
 已知:如图,AE是△ABC外角的平分线,且AE∥BC.
已知:如图,AE是△ABC外角的平分线,且AE∥BC.