题目内容
19．计算：$（{1-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}}）（{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}}）-（{1-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}-\frac{1}{5}}）（{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}}）$=$\frac{1}{5}$．分析 设$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=a，$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=b，再代入代数式进行计算即可．
解答 解：设$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=a，$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=b，
∵原式=[1-（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$）][$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$]-[1-（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$）]
=（1-a）b-（1-b）a
=b-ab-a+ab
=b-a，
∴原式=（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$）-（$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$）
=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$
=$\frac{1}{5}$．
故答案为：$\frac{1}{5}$．
点评 本题考查的是有理数的混合运算，熟知有理数混合运算的法则是解答此题的关键．
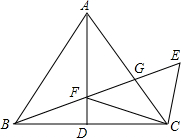如图，△ABC中，AB=AC，点D为BC边中点，CE∥AB，BE分别交AD、AC于点F、G，连接FC．求证：
如图，△ABC中，AB=AC=13，BC=10
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．若∠B=30°，CD=1，则BD的长为2．
如图，△ABC中，∠ACB=90°，AC=BC，点D、E分别在AB、BC上，且CD=DE，作EF⊥AB于点F．若AD=4，BF=2，求△CDE的面积．