题目内容
在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.
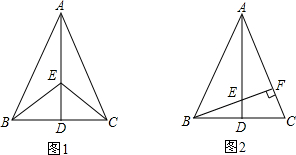
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)成立,根据等腰三角形的性质就可以求出∠BAE=∠CAE,再证明△ABE≌△ACE就可以得出结论;
(2)成立,由BF⊥AC,∠BAC=45°就可以求出AF=BF,在由条件证明△AEF≌△BCF就可以得出结论.
(2)成立,由BF⊥AC,∠BAC=45°就可以求出AF=BF,在由条件证明△AEF≌△BCF就可以得出结论.
解答:解:(1)成立.
理由:
∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中,
∴△ABE≌△ACE( SAS )
∴BE=CE.
(2)成立.
理由:
∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF…
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,
.
∴△AEF≌△BCF( AAS ),
∴EF=CF.
理由:
∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中,
|
∴△ABE≌△ACE( SAS )
∴BE=CE.
(2)成立.
理由:
∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF…
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,
|
∴△AEF≌△BCF( AAS ),
∴EF=CF.
点评:不同考查了中点的性质的运用,全等三角形的判定性质的运用,等腰三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 在淮南市发出创建文明城的倡议后,我校的小华与小明同学便积极的行动起来,他们在上体育课时发现操场上有块如图1所示的空地,经测量,在△ABC中,∠C=90°,AC=6m,BC=8m,他们向学校建议由他们来设计绿化方案:
在淮南市发出创建文明城的倡议后,我校的小华与小明同学便积极的行动起来,他们在上体育课时发现操场上有块如图1所示的空地,经测量,在△ABC中,∠C=90°,AC=6m,BC=8m,他们向学校建议由他们来设计绿化方案: 如图,已知A(3,-4),B(4,-3),C(5,0),求四边形ABCO的面积.
如图,已知A(3,-4),B(4,-3),C(5,0),求四边形ABCO的面积. 有理数a、b在数轴上位置如图所示,试化简|1-3b|+2|2+b|-|3b-2|.
有理数a、b在数轴上位置如图所示,试化简|1-3b|+2|2+b|-|3b-2|. 如图,l1反映了某公司产品的销售收入y1(元)与销售量x(吨)的关系,l2反映了该公司产品的销售成本y2(元)与销售量x(吨)之间的关系,根据图象填空:
如图,l1反映了某公司产品的销售收入y1(元)与销售量x(吨)的关系,l2反映了该公司产品的销售成本y2(元)与销售量x(吨)之间的关系,根据图象填空: