题目内容
 如图,l1反映了某公司产品的销售收入y1(元)与销售量x(吨)的关系,l2反映了该公司产品的销售成本y2(元)与销售量x(吨)之间的关系,根据图象填空:
如图,l1反映了某公司产品的销售收入y1(元)与销售量x(吨)的关系,l2反映了该公司产品的销售成本y2(元)与销售量x(吨)之间的关系,根据图象填空:(1)当销售量等于
当销售量
当销售量
(2)l1对应的函数表达式是
(3)求利润w(元)(销售收入-销售成本)与销售量x(吨)之间的函数关系式.
考点:一次函数的应用
专题:
分析:(1)利用图象交点得出公司盈利以及公司亏损情况;
(2)利用待定系数法求一次函数解析式即可;
(3)首先求出l2对应的函数关系式,进而得出w=y1-y2求出即可.
(2)利用待定系数法求一次函数解析式即可;
(3)首先求出l2对应的函数关系式,进而得出w=y1-y2求出即可.
解答:解:(1)如图所示:当销售量等于4吨时,利润为零(收入等于成本);
当销售量大于4吨时,该公司盈利(收入大于成本);
当销售量小于4吨时,该公司亏损(收入小于成本);
故答案为:4、大于4、小于4;
(2)将(4,4000)代入y1=ax,
∴4000=4a,
解得;a=1000,
∴l1对应的函数表达式是:y1=1000x;
故答案为:y1=1000x;
(3)设l2对应的函数关系式为y2=kx+b,
∵l2过点(0,2000),
∴b=2000,
又∵l2过点(4,4000),
∴4000=4k+2000,
解得:k=500,
所以y2=500x+2000,
又∵w=y1-y2=1000x-(500x+2000)
∴w=500x-2000.
当销售量大于4吨时,该公司盈利(收入大于成本);
当销售量小于4吨时,该公司亏损(收入小于成本);
故答案为:4、大于4、小于4;
(2)将(4,4000)代入y1=ax,
∴4000=4a,
解得;a=1000,
∴l1对应的函数表达式是:y1=1000x;
故答案为:y1=1000x;
(3)设l2对应的函数关系式为y2=kx+b,
∵l2过点(0,2000),
∴b=2000,
又∵l2过点(4,4000),
∴4000=4k+2000,
解得:k=500,
所以y2=500x+2000,
又∵w=y1-y2=1000x-(500x+2000)
∴w=500x-2000.
点评:此题主要考查了一次函数的应用,熟练利用数形结合得出是解题关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
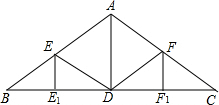 已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.
已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.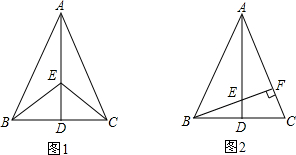
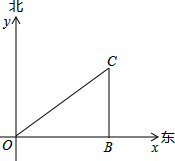 2012年4月中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
2012年4月中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).