题目内容
解方程
①x2-4x-3=0
②(x-3)2+2x(x-3)=0
③x2+6x+6=0
④(2x-3)2-5(2x-3)+6=0
⑤(3x+2)2=4(x-3)2
⑥12x2-x+6=0.
①x2-4x-3=0
②(x-3)2+2x(x-3)=0
③x2+6x+6=0
④(2x-3)2-5(2x-3)+6=0
⑤(3x+2)2=4(x-3)2
⑥12x2-x+6=0.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:①利用配方法求解即可,
②利用因式分解法法求解即可,
③利用配方法求解即可,
④利用因式分解法法求解即可,
⑤利用因式分解法法求解即可,
⑥根据△=(-1)2-4×12×6<0,即可得出方程无解.
②利用因式分解法法求解即可,
③利用配方法求解即可,
④利用因式分解法法求解即可,
⑤利用因式分解法法求解即可,
⑥根据△=(-1)2-4×12×6<0,即可得出方程无解.
解答:解:①∵x2-4x-3=0,
∴x2-4x=3,
∴x2-4x+4=3+4,
∴(x-2)2=7,
∴x-2=±
,
∴x1=2+
,x2=2-
;
②∵(x-3)2+2x(x-3)=0,
∴(x-3)(x-3+2x)=0,
∴(x-3)(3x-3)=0,
∴x-3=0,3x-3=0,
∴x1=3,x2=1;
③∵x2+6x+6=0,
∴x2+6x=-6,
∴x2+6x+9=-6+9,
∴(x+3)2=3,
∴x+3=±
,
∴x1=-3+
,x2=-3-
;
④∵(2x-3)2-5(2x-3)+6=0,
∴[(2x-3)-2][(2x-3)-3]=0,
∴(2x-5)(2x-6)=0,
∴2x-5=0或2x-6=0,
∴x1=
,x2=3;
⑤∵(3x+2)2=4(x-3)2,
∴(3x+2)2-4(x-3)2=0,
∴[(3x+2)+2(x-3)][(3x+2)-2(x-3)]=0,
∴(5x-4)(x+8)=0,
∴5x-4=0,x+8=0,
∴x1=
,x2=-8;
⑥∵12x2-x+6=0,
∴△=(-1)2-4×12×6<0,
∴此方程无解.
∴x2-4x=3,
∴x2-4x+4=3+4,
∴(x-2)2=7,
∴x-2=±
| 7 |
∴x1=2+
| 7 |
| 7 |
②∵(x-3)2+2x(x-3)=0,
∴(x-3)(x-3+2x)=0,
∴(x-3)(3x-3)=0,
∴x-3=0,3x-3=0,
∴x1=3,x2=1;
③∵x2+6x+6=0,
∴x2+6x=-6,
∴x2+6x+9=-6+9,
∴(x+3)2=3,
∴x+3=±
| 3 |
∴x1=-3+
| 3 |
| 3 |
④∵(2x-3)2-5(2x-3)+6=0,
∴[(2x-3)-2][(2x-3)-3]=0,
∴(2x-5)(2x-6)=0,
∴2x-5=0或2x-6=0,
∴x1=
| 5 |
| 2 |
⑤∵(3x+2)2=4(x-3)2,
∴(3x+2)2-4(x-3)2=0,
∴[(3x+2)+2(x-3)][(3x+2)-2(x-3)]=0,
∴(5x-4)(x+8)=0,
∴5x-4=0,x+8=0,
∴x1=
| 4 |
| 5 |
⑥∵12x2-x+6=0,
∴△=(-1)2-4×12×6<0,
∴此方程无解.
点评:此题考查了一元二次方程的解法,关键是根据方程的特点选择合适的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:如图,A、E、F、B四点在一条直线上,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:(1)CE=DF;(2)CE∥DF.
已知:如图,A、E、F、B四点在一条直线上,AC⊥CE,BD⊥DF,AE=BF,AC=BD.求证:(1)CE=DF;(2)CE∥DF. 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对2个面上的代数式的值相等,求a,x,y的值.
如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对2个面上的代数式的值相等,求a,x,y的值.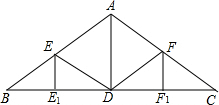 已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.
已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.