题目内容
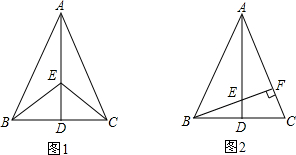
 在淮南市发出创建文明城的倡议后,我校的小华与小明同学便积极的行动起来,他们在上体育课时发现操场上有块如图1所示的空地,经测量,在△ABC中,∠C=90°,AC=6m,BC=8m,他们向学校建议由他们来设计绿化方案:
在淮南市发出创建文明城的倡议后,我校的小华与小明同学便积极的行动起来,他们在上体育课时发现操场上有块如图1所示的空地,经测量,在△ABC中,∠C=90°,AC=6m,BC=8m,他们向学校建议由他们来设计绿化方案:【设计方案一】、想将这块地分割成面积相等的4块来种植不同的花草,请你在备用图2中设计出他们可能设计的一种方案来.
【设计方案二】、他们想让靠近AB边的部分空地预留出16m2来铺上草坪,余下的8m2种花,于是小明(点P)从点A出发沿边AC向点C以1m/s的速度移动,小华(点Q)从C点出发沿CB边向点B以2m/s的速度移动.如果他们从A、B两点同时出发,几秒钟后,可获得△PCQ的面积为8平方米?
【设计方案三】、他们想用方案二的同样办法,来获得△PCQ的面积等于△ABC的面积的一半.你觉得他们能办到吗?若行,求出运动的时间;若不行,说明理由.
考点:一元二次方程的应用
专题:
分析:【设计方案一】根据三角形的中线平分三角形的面积画图即可;
【设计方案二】首先设x秒钟后,可获得△PCQ的面积为8平方米,然后再表示出PC和QC长,利用三角形的面积公式可得
(6-x)×2x=8,再解方程即可;
【设计方案三】设a秒钟后,可获得△PCQ的面积为8平方米,根据△PCQ的面积等于△ABC的面积的一半列出方程,然后再根据根的判别式进行计算即可.
【设计方案二】首先设x秒钟后,可获得△PCQ的面积为8平方米,然后再表示出PC和QC长,利用三角形的面积公式可得
| 1 |
| 2 |
【设计方案三】设a秒钟后,可获得△PCQ的面积为8平方米,根据△PCQ的面积等于△ABC的面积的一半列出方程,然后再根据根的判别式进行计算即可.
解答: 解:【设计方案一】如图所示:分别找出三边中点E、F、H,再连接CE、EF、EH即可;
解:【设计方案一】如图所示:分别找出三边中点E、F、H,再连接CE、EF、EH即可;
【设计方案二】设x秒钟后,可获得△PCQ的面积为8平方米.
(6-x)×2x=8,
化简得x2-6x+8=0,
解得x1=2,x2=4,
经检验x1=2,x2=4均符合要求,
答:2秒钟或4秒钟后,可获得△PCQ的面积为8平方米.
【设计方案三】设a秒钟后,可获得△PCQ的面积为8平方米,由题意得:
(6-a)×2a=12,
化简得:a2-6a+12=0,
△=36-4×12<0,方程无实数根,
所以不能获得△PCQ的面积等于△ABC的面积的一半.
 解:【设计方案一】如图所示:分别找出三边中点E、F、H,再连接CE、EF、EH即可;
解:【设计方案一】如图所示:分别找出三边中点E、F、H,再连接CE、EF、EH即可;【设计方案二】设x秒钟后,可获得△PCQ的面积为8平方米.
| 1 |
| 2 |
化简得x2-6x+8=0,
解得x1=2,x2=4,
经检验x1=2,x2=4均符合要求,
答:2秒钟或4秒钟后,可获得△PCQ的面积为8平方米.
【设计方案三】设a秒钟后,可获得△PCQ的面积为8平方米,由题意得:
| 1 |
| 2 |
化简得:a2-6a+12=0,
△=36-4×12<0,方程无实数根,
所以不能获得△PCQ的面积等于△ABC的面积的一半.
点评:此题主要考查了一元二次方程的解法,关键是正确理解题意,找出题目中的等量关系,列出方程.

练习册系列答案
相关题目
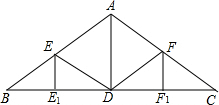 已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.
已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.