题目内容
20．如图中的虚线网格为菱形网格，每一个小菱形的面积均为1，网格中虚线的交点称为格点，顶点都在格点的多边形称为格点多边形，如：格点?ABCD的面积是6．（1）格点△PMN的面积是6．
（2）格点四边形EFGH的面积是28．
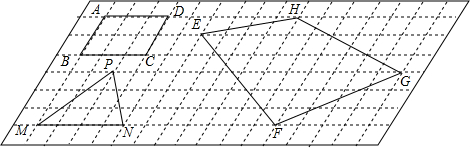
分析 （1）根据S△PMN=$\frac{1}{2}$•S平行四边形MNEF计算即可；
（2）根据S四边形EFGH=S平行四边形LJKT-S△LEH-S△HTG-S△FKG-S△EFJ计算即可．
解答 解：（1）如图，
S△PMN=$\frac{1}{2}$•S平行四边形MNEF=$\frac{1}{2}$×12=6，
故答案为6．
（2）S四边形EFGH=S平行四边形LJKT-S△LEH-S△HTG-S△FKG-S△EFJ
=60-2-9-6-15=28，
故答案为28
点评 本题考查菱形的性质、平行四边形的性质等知识，解题的关键是学会用分割法求面积，属于中考常考题型．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8．已知m是方程2x-1=5的解，则代数式3m-2的值为（ ）
| A． | -11 | B． | -8 | C． | 4 | D． | 7 |
15．某校在“6•26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛，赛后随机抽取了部分学生成绩进行统计，制作如表频数分布表和频数分布直方图，请根据图表提供的信息，解答下列问题：
（1）表中a=8，b=0.3，并补全直方图
（2）若用扇形统计图描述此成绩分布情况，则分数段80≤x＜100对应扇形的圆心角度数是144°；
（3）请估计该年级分数在60≤x＜100的学生有多少人？
| 少分数段（x表示分数） | 频数 | 频率 |
| 50≤x＜60 | 4 | 0.1 |
| 60≤x＜70 | a | 0.2 |
| 70≤x＜80 | 12 | b |
| 80≤x＜90 | 10 | 0.25 |
| 90≤x＜100 | 6 | 0.15 |
（1）表中a=8，b=0.3，并补全直方图
（2）若用扇形统计图描述此成绩分布情况，则分数段80≤x＜100对应扇形的圆心角度数是144°；
（3）请估计该年级分数在60≤x＜100的学生有多少人？
12．如果用A表示事件“若a＞b，则a+c＞b+c”，用P（A）表示“事件A发生的概率”，那么下列结论中正确的是（ ）
| A． | P（A）=1 | B． | P（A）=0 | C． | 0＜P（A）＜1 | D． | P（A）＞1 |
9．小聪用100元钱去购买笔记本和钢笔共15件，已知每本笔记本5元，每支钢笔7元，小聪最多能买（ ）支钢笔．
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |