题目内容
10.如果不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a≥2}\\{2x-b<3}\end{array}\right.$的解集是0≤x<1,那么a=2,b=-1.分析 先用a,b表示出不等式组的解集,再根据不等式组的解集为0≤x<1求出a,b的值.
解答 解:$\left\{\begin{array}{l}{\frac{x}{2}+a≥2(1)}\\{2x-b<3(2)}\end{array}\right.$,
解(1)得:x≥4-2a.
解(2)得:x<$\frac{b+3}{2}$.
∵不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a≥2}\\{2x-b<3}\end{array}\right.$的解集是0≤x<1,
∴4-2a=0,$\frac{b+3}{2}$=1,
解得a=2,b=-1.
故答案是:2;-1.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
5.若方程组$\left\{\begin{array}{l}{1998x+2006y=2007}\\{(|a|-2)z+5x=5}\end{array}\right.$是二元一次方程组,则a等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
15.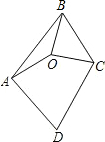 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
 如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )
如图,已知O是四边形ABCD内一点,OA=OB=OC,∠ABC=∠ADC=70°,则∠DAO+∠DCO的大小是( )| A. | 70° | B. | 110° | C. | 140° | D. | 150° |
 如图所示,则x的取值范围是-3<x≤2.
如图所示,则x的取值范围是-3<x≤2.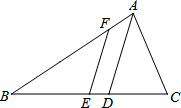 如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.
如图,在△ABC中,∠C=2∠B,AD平分∠BAC交BC于点D,点E为BC中点,EF∥AD交AB于点F.若BF=4AF,CD=$\frac{12}{5}$,则AC=$\frac{18}{5}$.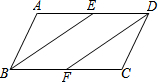 如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.
如图,在?ABCD中,若点E、F是AD、BC的中点,连接BE、DF.