题目内容
15．
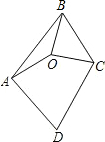如图，已知O是四边形ABCD内一点，OA=OB=OC，∠ABC=∠ADC=70°，则∠DAO+∠DCO的大小是（ ）| A． | 70° | B． | 110° | C． | 140° | D． | 150° |
分析 在四边形ADCO中，求出∠AOC即可解决问题，根据圆心角与圆周角的关系可以求出∠AOC．
解答 解：如图，∵OA=OB=OC，∠ABC=∠ADC=70°
∴∠ABO=∠BAO，∠OBC=∠OCB，
∴∠AOB+∠BOC=360°-2（∠ABO+∠OBC）=220°
∴∠AOC=360°-220°=140°，
∵∠OAD+∠ADC+∠OCD+∠AOC=360°，
∴∠DAO+∠DCO=150°．
故选D．
点评 本题考查等腰三角形的性质，四边形内角和为360°，求出∠AOC是解题的关键，属于中考常考题型．
练习册系列答案
全能测控期末小状元系列答案
相关题目
10．如果不等式组$\left\{\begin{array}{l}{\frac{x}{2}+a≥2}\\{2x-b＜3}\end{array}\right.$的解集是0≤x＜1，那么a=2，b=-1．
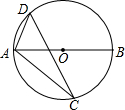如图，AB是⊙O的直径，△ACD内接于⊙O，若∠BAC=42°，则∠ADC=48°．
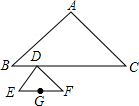如图，点D是Rt△ABC斜边BC上一动点，以D为直角顶角作Rt△DEF，点G是EF中点，连接AG，若AB=AC=2，DE=DF=1．设AG=x，则x的最小值是$\frac{3\sqrt{2}}{2}$．
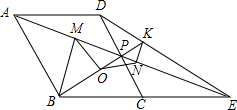如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点，作BM⊥AE于点M，作KN⊥AE于点N，连结MO、NO，以下四个结论：①△OMN是等腰三角形；②tan∠OMN=$\frac{\sqrt{3}}{3}$；③BP=4PK；④PM•PA=3PD2，其中正确的是（ ）