题目内容
 如图,AB是⊙O的切线,∠O=60°,OA=10,则⊙O的半径长为
如图,AB是⊙O的切线,∠O=60°,OA=10,则⊙O的半径长为考点:切线的性质
专题:
分析:因为AB是⊙O的切线,则OA就是圆的半径,再解直角三角形OAB即可.
解答:解:∵AB是⊙O的切线.OA就是圆的半径.
∴∠AOB=90°,
∴OA=OB•sin(90°-60°)=10×
=5.
故答案为:5.
∴∠AOB=90°,
∴OA=OB•sin(90°-60°)=10×
| 1 |
| 2 |
故答案为:5.
点评:本题考查了切线的性质,根据AB是切线,得到OA是圆的半径是解决本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
函数y=
的自变量x的取值范围是( )
| 1 |
| x-1 |
| A、x≠0 | B、x≠1 |
| C、x≥1 | D、x≤1 |
下列长度的三条线段能组成一个三角形的是( )
| A、1,2,1 | ||
B、
| ||
| C、2,3,4 | ||
| D、3,4,8 |
 如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,∠C=∠D=135°,求∠A的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥DE,BC∥EF,∠C=∠D=135°,求∠A的度数.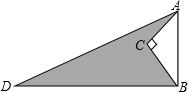 如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=
如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= 已知:如图,AB=AC,BD=CD,DE⊥AB,垂足为E,DF⊥AC,垂足为F.求证:DE=DF.
已知:如图,AB=AC,BD=CD,DE⊥AB,垂足为E,DF⊥AC,垂足为F.求证:DE=DF.
 分别求出图中∠A,∠B的正弦值、余弦值和正切值.
分别求出图中∠A,∠B的正弦值、余弦值和正切值.