题目内容
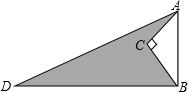 如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=
如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=考点:勾股定理的逆定理,勾股定理
专题:
分析:先利用勾股定理求出AB,然后利用勾股定理的逆定理判断出△ABD是直角三角形,然后分别求出两个三角形的面积,相减即可求出阴影部分的面积.
解答:解:在RT△ABC中,AB=
=5,
∵AD=13,BD=12,
∴AB2+BD2=AD2,即可判断△ABD为直角三角形,
阴影部分的面积=
AB×BD-
BC×AC=30-6=24.
答:阴影部分的面积=24.
故答案为:24.
| AC2+BC2 |
∵AD=13,BD=12,
∴AB2+BD2=AD2,即可判断△ABD为直角三角形,
阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
答:阴影部分的面积=24.
故答案为:24.
点评:此题考查了勾股定理、勾股定理的逆定理,属于基础题,解答本题的关键是判断出三角形ABD为直角三角形.

练习册系列答案
相关题目
直线l与直线y=-2x+3平行,并且与直线y=2x-3交于y轴的同一点,则直线l的解析式为( )
| A、y=-2x-3 |
| B、y=-2x+3 |
| C、y=2x-3 |
| D、y=2x+3 |
卫生部门为了控制前段时间红眼病的流行传染,对该种传染病进行研究发现,若一人患了该病,经过两轮传染后共有121人患了该病.若按这样的传染速度,第三轮传染后我们统计发现有2662人患了该病,则最开始有( )人患了该病.
| A、1 | B、2 | C、3 | D、4 |
直线l外一点P与直线l上两点的连线段长分别为4cm,6cm,则点P到直线l的距离是( )
| A、不超过4cm | B、4cm |
| C、6cm | D、不少于6cm |
若
+|y+1|=0,则(x+y)2015的值是( )
| x-2 |
| A、1 | B、-1 | C、2 | D、-2 |
 如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).
如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹). 如图,AB=AC,BD=CD,延长DB至M,使MB=
如图,AB=AC,BD=CD,延长DB至M,使MB=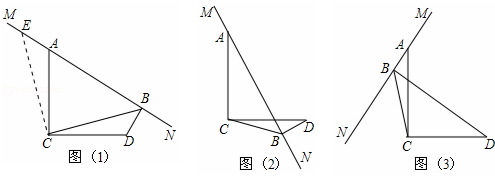
 如图,AB是⊙O的切线,∠O=60°,OA=10,则⊙O的半径长为
如图,AB是⊙O的切线,∠O=60°,OA=10,则⊙O的半径长为