题目内容
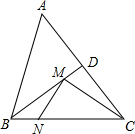如图，在等腰△ABC中，AB=BC=5，AC=6，∠ABC的平分线交AC于点D，M、N分别是BD和BC上的动点，则CM+MN的最小值是考点：轴对称-最短路线问题
专题：
分析：过点A作AN⊥BC于N交BD于M，根据轴对称和由垂线段最短确定最短路线问题，AN的长度即为BM+MN的最小值，求得△ANC∽△BDC，根据相似三角形对应边成比例求解即可．
解答：解：如图，由垂线段最短，过点A作AN⊥BC于N交BD于M，AN最短，
∵△ABC是等腰三角形，BD是∠ABC的平分线，
∴BD垂直平分AC，
∴A、C关于BD对称，
由轴对称性质，AM=CM，
∴CM+MN=AM+MN=AN，
∵BD⊥AC，AD=DC，
∴DC=3，
∴BD=
=4，
∵∠ANC=∠BDC=90°，∠ACN=∠BCD，
∴△ANC∽△BDC，
∴
=
，即
=
，解得AN=
，
∴CM+MN的最小值是
．
故答案为：
．
∵△ABC是等腰三角形，BD是∠ABC的平分线，
∴BD垂直平分AC，
∴A、C关于BD对称，
由轴对称性质，AM=CM，
∴CM+MN=AM+MN=AN，
∵BD⊥AC，AD=DC，
∴DC=3，
∴BD=
| 52-32 |
∵∠ANC=∠BDC=90°，∠ACN=∠BCD，
∴△ANC∽△BDC，
∴
| AN |
| BD |
| AC |
| BC |
| AN |
| 4 |
| 6 |
| 5 |
| 24 |
| 5 |
∴CM+MN的最小值是
| 24 |
| 5 |
故答案为：
| 24 |
| 5 |
点评：本题考查了轴对称的性质，垂线段最短，相似三角形的判定与性质，确定出点M、N的位置是解题的关键，作出图形更形象直观．
练习册系列答案
优等生题库系列答案
相关题目
如图，AB是⊙O的直径，四边形ABCD内接于⊙O，AD、BC的延长线交于点E．求证：ED•EA=EB•EC．
如图，△ABC中，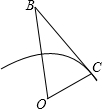
“欲穷千里目，更上一层楼”是唐代诗人王之涣的不朽诗句．不过我们现在地球上看到据观测点1000米处的景色，“更上一层楼”中的楼到底有多高呢？存在这样的楼房吗？（设
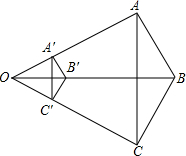如图，△ABC的三条边与△A′B′C′的三条边满足A′B′∥AB，B′C′∥BC，A′C′∥AC，且OB=3OB′，△ABC的面积与△A′B′C′的面积之间的关系？