题目内容
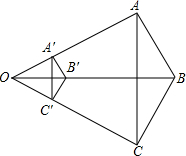如图，△ABC的三条边与△A′B′C′的三条边满足A′B′∥AB，B′C′∥BC，A′C′∥AC，且OB=3OB′，△ABC的面积与△A′B′C′的面积之间的关系？考点：相似三角形的判定与性质
专题：
分析：由条件可知△A′B′C′和△ABC是位似图形，且位似比为1：3，利用位似图形的性质可知△A′B′C′∽△ABC，可求得结论．
解答：解：∵A′B′∥AB，B′C′∥BC，A′C′∥AC，
∴知△A′B′C′和△ABC是位似图形，且位似比为1：3，
∴△A′B′C′∽△ABC，相似比为1：3，
∴
=
，
∴S△ABC=9S△A′B′C′．
∴知△A′B′C′和△ABC是位似图形，且位似比为1：3，
∴△A′B′C′∽△ABC，相似比为1：3，
∴
| S△A′B′C′ |
| S△ABC |
| 1 |
| 9 |
∴S△ABC=9S△A′B′C′．
点评：本题主要考查相似三角形的判定和性质，掌握位似图形的定义和性质是解题的关键．
练习册系列答案
相关题目
从2009年1月1日起，重庆市将房产交易契税，由原来的1%降低到0.5%．本季度房产交易契税为104040000元，用科学记数法表示为（ ）
| A、10.404×108元 |
| B、0.10404×108元 |
| C、1.0404×109元 |
| D、1.0404×108元 |
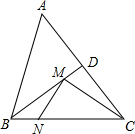如图，在等腰△ABC中，AB=BC=5，AC=6，∠ABC的平分线交AC于点D，M、N分别是BD和BC上的动点，则CM+MN的最小值是
如图所示，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，求