题目内容
如图，AB是⊙O的直径，四边形ABCD内接于⊙O，AD、BC的延长线交于点E．求证：ED•EA=EB•EC．考点：切割线定理
专题：证明题
分析：根据圆内接四边形的性质得到∠EDC=∠B，于是可证明△EDC∽△EBA，则ED：EB=EC：EA，然后利用比例的性质即可得到结论．
解答：证明：∵四边形ABCD内接于⊙O，
∴∠EDC=∠B，
而∠DEC=∠BEA，
∴△EDC∽△EBA，
∴ED：EB=EC：EA，
∴ED•EA=EB•EC．
∴∠EDC=∠B，
而∠DEC=∠BEA，
∴△EDC∽△EBA，
∴ED：EB=EC：EA，
∴ED•EA=EB•EC．
点评：本题考查了切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项；从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等． 此题实际上证明了切割线定理．
练习册系列答案
相关题目
|
| ||
|
| A、m＜1且m≠0 |
| B、m＞0且m≠1 |
| C、0＜m＜1 |
| D、0＜m≤1 |
某商店的一商品因需求量大，经营者对该商品进行了两次提价，每次提价10%；后经市场物价调整，又一次降价20%，已知提价前的商品价格为a，则该商品的最终价格为（ ）
| A、1.04a | B、a |
| C、0.96a | D、0.968a |
从2009年1月1日起，重庆市将房产交易契税，由原来的1%降低到0.5%．本季度房产交易契税为104040000元，用科学记数法表示为（ ）
| A、10.404×108元 |
| B、0.10404×108元 |
| C、1.0404×109元 |
| D、1.0404×108元 |
如图，若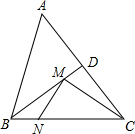
如图，在等腰△ABC中，AB=BC=5，AC=6，∠ABC的平分线交AC于点D，M、N分别是BD和BC上的动点，则CM+MN的最小值是