题目内容
如图，△ABC中，| AD |
| DB |
| AE |
| EC |
（1）证明：
| DB |
| AB |
| EC |
| AC |
（2）若AB=12，AE=6，EC=4，求AD的长．
考点：相似三角形的判定与性质
专题：
分析：（1）由条件可得到DE∥BC，再利用平行线分线段成比例可得到结论；
（2）利用
=
，且BD=AB-AD，代入可求得AD．
（2）利用
| AD |
| DB |
| AE |
| EC |
解答：（1）证明：∵
=
，
∴
=
，即
=
，
∴△ADE∽△ABC，
∴∠ADE=∠ABC，
∴DE∥BC，
∴
=
；
（2）解：∵
=
，且BD=AB-AD=12-AD，
∴
=
，
解得AD=7.2．
| AD |
| DB |
| AE |
| EC |
∴
| AD |
| AD+DB |
| AE |
| AE+EC |
| AD |
| AB |
| AE |
| AC |
∴△ADE∽△ABC，
∴∠ADE=∠ABC，
∴DE∥BC，
∴
| DB |
| AB |
| EC |
| AC |
（2）解：∵
| AD |
| DB |
| AE |
| EC |
∴
| AD |
| 12-AD |
| 6 |
| 4 |
解得AD=7.2．
点评：本题主要考查相似三角形的判定和性质，先证得DE∥BC是解题的关键，注意方程思想的应用．
练习册系列答案
相关题目
如图，DE∥BC．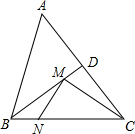
如图，在等腰△ABC中，AB=BC=5，AC=6，∠ABC的平分线交AC于点D，M、N分别是BD和BC上的动点，则CM+MN的最小值是
如图所示，①图中∠1表示成∠A，②图中∠2表示成∠D；③图中∠3表示成∠C，这样的表示方法对不对？如果不对，应怎样改正？
如图所示，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，求