题目内容
 “欲穷千里目,更上一层楼”是唐代诗人王之涣的不朽诗句.不过我们现在地球上看到据观测点1000米处的景色,“更上一层楼”中的楼到底有多高呢?存在这样的楼房吗?(设
“欲穷千里目,更上一层楼”是唐代诗人王之涣的不朽诗句.不过我们现在地球上看到据观测点1000米处的景色,“更上一层楼”中的楼到底有多高呢?存在这样的楼房吗?(设 |
| AC |
 |
| AC |
考点:解直角三角形的应用
专题:
分析:根据题意首先求出弧AC对应的圆心角为α 的度数,进而求出OB的长,进而得出楼高.
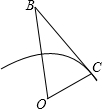
解答: 解:如图所示:
解:如图所示:
设弧AC对应的圆心角为α,
α=
×360°≈4.5°,
BC为弧AC的切线,即BC⊥OC,
OB=
=
=6389.7≈6390(km),
楼高AB=OB-OA=6390-6370=20(km).
答:楼高为20km,不存在这样高的楼.
 解:如图所示:
解:如图所示:设弧AC对应的圆心角为α,
α=
1000×
| ||
| 2π×6370 |
BC为弧AC的切线,即BC⊥OC,
OB=
| CO |
| cosα |
| 6370 |
| cos4.5° |
楼高AB=OB-OA=6390-6370=20(km).
答:楼高为20km,不存在这样高的楼.
点评:此题主要考查了解直角三角形的应用,根据题意得出α的度数是解题关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
某商店的一商品因需求量大,经营者对该商品进行了两次提价,每次提价10%;后经市场物价调整,又一次降价20%,已知提价前的商品价格为a,则该商品的最终价格为( )
| A、1.04a | B、a |
| C、0.96a | D、0.968a |
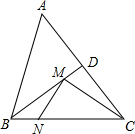 如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是
如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是 如图,以点P为位似中心,将五角星缩小为原来的
如图,以点P为位似中心,将五角星缩小为原来的
 要在两个城镇A、B的附近修建一个加油站.如图,按设计要求,加油
要在两个城镇A、B的附近修建一个加油站.如图,按设计要求,加油