题目内容
已知tanα+(tanα)-1=3,α为锐角,则tan2α+(tanα)-2= .
考点:同角三角函数的关系
专题:
分析:直接利用完全平方公式求出即可.
解答:解:∵tanα+(tanα)-1=3,
∴[tanα+(tanα)-1]2=9,
∴tan2α+(tanα)-2+2=9,
∴tan2α+(tanα)-2=7.
故答案为:7.
∴[tanα+(tanα)-1]2=9,
∴tan2α+(tanα)-2+2=9,
∴tan2α+(tanα)-2=7.
故答案为:7.
点评:此题主要考查了同角的三角函数关系,正确利用完全平方公式求出是解题关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 如图,若
如图,若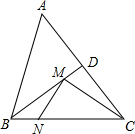 如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是
如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是 如图,以点P为位似中心,将五角星缩小为原来的
如图,以点P为位似中心,将五角星缩小为原来的