题目内容
14.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )| A. | 42 | B. | 32 | C. | 42或32 | D. | 42或37 |
分析 本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
解答 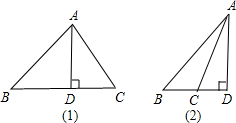 解:此题应分两种情况说明:
解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=9,
在Rt△ACD中,
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=9,
在Rt△ACD中,CD=5,
∴BC=9-5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故选:C.
点评 此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.

练习册系列答案
相关题目
4.下列方程中是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-3=x2+2x-1 | C. | x2=0 | D. | x2-2xy-5y2=0 |
19. 如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
 如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
6.下列说法中错误的是( )
| A. | 正分数、负分数统称分数 | B. | 零是整数,但不是分数 | ||
| C. | 正整数、负整数统称整数 | D. | 零既不是正数,也不是负数 |
4.下列方程不是一元二次方程的是( )
| A. | $\sqrt{3}{x^2}+2x+1=0$ | B. | 0.1x2-0.5x+1.8=0 | ||
| C. | $\frac{1}{2}{x^2}=1-\frac{3}{5}x$ | D. | x2+x-1=(x+1)2 |
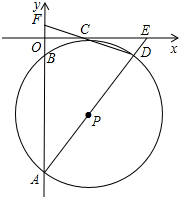 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,2),点D的坐标为(6,-2).
如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,2),点D的坐标为(6,-2).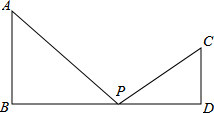 如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.
如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.