题目内容
3.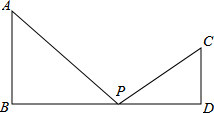 如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.
如图所示,AB⊥BD,CD⊥BD,AB=6,CD=4,BD=k,点P在BD上移动,保持∠APC=90°,但不与点B和点D重合.(1)当k=14时,请问在BD上存在多少个P点,使以P,C,D为顶点的三角形与△ABP相似?并求BP的长.
(2)已知在BD上至少存在一个P点,使以P,C,D为顶点的三角形与△ABP相似,求k的取值范围.
分析 (1)设出BP=xcm,由BD-BP=PD表示出PD的长,①若△ABP∽△PDC;②若△ABP∽△CDP;根据相似三角形的对应边成比例可得比例式,把各边的长代入即可列出关于x的方程,求出方程的解即可得到x的值,即为PB的长.
(2)由(1)①得出$\frac{6}{14-x}=\frac{x}{4}$,整理得:x2-14x+24=0,由根的判别式≥0即可得出结果.
解答 解:(1)由AB=6cm,CD=4cm,BD=14cm,
设BP=xcm,则PD=(14-x)cm,
①若△ABP∽△PDC,
则$\frac{AB}{PD}=\frac{BP}{CD}$,即$\frac{6}{14-x}=\frac{x}{4}$,
整理得:x2-14x+24=0,
解得:x1=2,x2=12,
所以BP=2cm或12cm时,△ABP∽△PDC;
②若△ABP∽△CDP,
则$\frac{AB}{CD}=\frac{BP}{DP}$,即$\frac{6}{4}=\frac{x}{14-x}$,
解得:x=8.4,
∴BP=8.4cm,
综上,BP=2cm或12cm或8.4cm时,△ABP∽△PDC.
即在BD上存在3个P点,使以P,C,D为顶点的三角形与△ABP相似,BP的长为8.4cm或12cm或2cm.
(2)由(1)①得:若△ABP∽△PDC,
则$\frac{AB}{PD}=\frac{BP}{CD}$,即$\frac{6}{k-x}=\frac{x}{4}$,
整理得:x2-kx+24=0,
当△=k2-96≥0(k>0)时,k≥4$\sqrt{6}$,
∴在BD上至少存在一个P点,使以P,C,D为顶点的三角形与△ABP相似,k的取值范围为k≥4$\sqrt{6}$.
点评 此题考查了相似三角形的判定与性质以及动点问题;熟练掌握相似三角形的判定与性质是解决问题的关键,注意分类讨论.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | 正数 | B. | 负数 | C. | 正数或零 | D. | 负数或零 |
| A. | 42 | B. | 32 | C. | 42或32 | D. | 42或37 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | π一定是正数 | B. | -a一定是负数 | C. | +a一定是正数 | D. | 3+a一定是正数 |
| A. | a3+a3=a6 | B. | (a3)3=a9 | C. | a3•a6=a18 | D. | 3a•6a=18a |
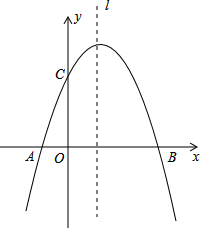 已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点