题目内容
19. 如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=8cm,OC⊥AB于点C,则OC=( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
分析 连接OB,构建直角△OCB,根据垂径定理得:BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,利用勾股定理可求OC的长.
解答  解:如图,连接OB,
解:如图,连接OB,
∵OC⊥AB,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
∵OB=5,
由勾股定理得:OC=$\sqrt{O{B}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3cm;
故选A.
点评 本题考查了垂径定理和勾股定理,明确垂直弦的直径平分这条弦,并且平分弦所对的两条弧;在圆中,常连接半径或作弦心距构建直角三角形,利用勾股定理求边长.

练习册系列答案
相关题目
9.对于-3.$\stackrel{•}{2}$7$\stackrel{•}{1}$,下列说法不正确的是( )
| A. | 是负数 | B. | 是分数 | C. | 是有理数 | D. | 是无理数 |
7. 用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )
用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )
 用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )
用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
14.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
| A. | 42 | B. | 32 | C. | 42或32 | D. | 42或37 |

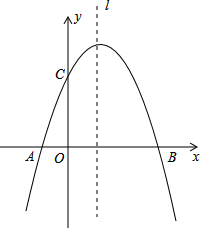 已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点