题目内容
2.已知一个两位数的十位数字是个位数字的2倍多1,将这个两位数的个位数字和十位改字交换位置后,得到新的两位数是原两位数减去2后的一半,求这个两位数.分析 首先设个位数字为x,则十位数字为(2x+1),则原两位数可表示为10(2x+1)+x,数字对调后所得两位数是[10x+(2x+1)],再根据“将两个数对调后得到的两位数是原两位数减去2后的一半”可得方程:[10x+(2x+1)]=$\frac{1}{2}$[10(2x+1)+x-2],解方程得到个位数,进而可得十位数字.
解答 解:设个位数字为x,则十位数字为(2x+1),
依题意得:[10x+(2x+1)]=$\frac{1}{2}$[10(2x+1)+x-2],
解得x=2,
则2x+1=5,
故这个两位数是52.
答:这个两位数是52.
点评 此题主要考查了一元一次方程的应用,关键是表示出原两位数与新的两位数,根据数之间的关系列出方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.⊙O的半径为10cm,点A到圆心O的距离OA=8cm,则点A与⊙O的位置关系为( )
| A. | 点A在圆上 | B. | 点A在圆内 | C. | 点A在圆外 | D. | 无法确定 |
13.如果一个数的绝对值是它的相反数,则这个数是( )
| A. | 正数 | B. | 负数 | C. | 正数或零 | D. | 负数或零 |
17.在(-1)3,-12016,-22,(-3)2这四个数中,最大的数( )
| A. | (-1)3 | B. | -12016 | C. | -22 | D. | (-3)2 |
7. 用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )
用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )
 用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )
用直尺和圆规作一个角等于已知角,如图,能得出∠O=∠O'的依据是( )| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
14.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )
| A. | 42 | B. | 32 | C. | 42或32 | D. | 42或37 |
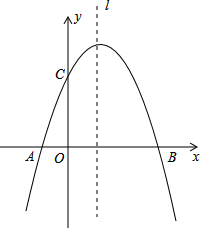 已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点