Question

2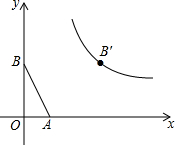．已知：如图，在平面直角坐标系中，点A（1，0），B（0，2），将点B沿x轴正方向平移3个单位长度得到对应点B′，点B′恰在反比例函数y=$\frac{k}{x}$（x＞0）的图象上．在同一平面内，是否存在这样的点P，以P为位似中心，将△AOB放大为原来的两倍后得到△DEF（即△DEF∽△AOB，且相似比为2），使得点D、F恰好在反比例函数y=$\frac{k}{x}$（x＞0）的图象上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

Answer 1

分析 △AOB放大为原来的两倍后得到△DEF，且△DEF∽△AOB，则点D和F一定在反比例函数图象上，设出P与D坐标，根据该相似三角形的对应边成比例列出比例式并解答．

解答 解：如图：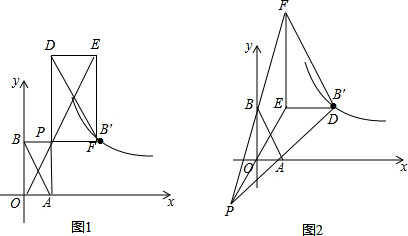

△AOB放大为原来的两倍后得到△DEF，且△DEF∽△AOB，则一定是D和F在反比例函数图象上，
设P的坐标是（e，f），设D的坐标是（c，d），
当P在AB的左侧时，$\frac{c-1}{1-e}$=2，且$\frac{d-0}{0-f}$=2，
解得：c=3-2e，d=-2f，
则（3-2e）•（-2f）=6，
设F的坐标是（g，h），则$\frac{g-0}{0-e}$=2，$\frac{h-2}{2-f}$=2，
整理得：g=-2e，h=6-2f．
则-2e•（6-2f）=6，
联立得：$\left\{\begin{array}{l}{（3-2e）•（-2f）=6}\\{-2e•（6-2f）=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{e=-1}\\{f=-2}\end{array}\right.$，或 $\left\{\begin{array}{l}{e=1}\\{f=2}\end{array}\right.$．
故P坐标为（-1，-2）或（1，2）．

点评 本题考查了反比例函数综合题．关键是利用反比例函数图象上点的坐标特征以及位似图形的性质．同时要注意x的取值范围，难度比较大．