题目内容
14.画出函数y=x2-4x-3的图象,根据图象回答下列问题:(1)图象与x轴交点的坐标是什么?
(2)方程x2-4x-3=0的解是什么?
(3)不等式x2-4x-3>0,x2-4x-3<0的解集分别是什么?
分析 确定二次函数的对称轴,以及与x轴的交点,与y轴的交点即可作出函数的图象,根据图象解决问题.
(1)根据图象即可求解;
(2)方程的解就是与x轴的交点的横坐标,据此可求解;
(3)根据函数图象即可直接求解.
解答 解:函数y=x2-4x-3的图象开口向上,与x轴的交点是(2+$\sqrt{7}$,0),(2-$\sqrt{7}$,0),对称轴是x=2. .
.
(1)与x轴的交点是(2+$\sqrt{7}$,0),(2-$\sqrt{7}$,0);
(2)方程x2-4x-3=0的解是x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$;
(3)不等式x2-4x-3>0的解集是:x<2-$\sqrt{7}$或x>2+$\sqrt{7}$;
x2-4x-3<0的解集是2-$\sqrt{7}$<x<2+$\sqrt{7}$.
点评 本题考查了二次函数与x轴的交点以及函数图象的作法,正确理解函数值与方程、不等式的关系是关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
4.若$\root{3}{x}$+$\root{3}{-y}$=0,则x与y的关系是( )
| A. | x+y=0 | B. | x-y=0 | C. | x•y=0 | D. | x=y=0 |
6.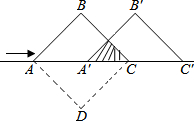 如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )
如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )
 如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )
如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )| A. | 2cm | B. | $2\sqrt{2}+2$cm | C. | $\sqrt{2}$cm | D. | $2\sqrt{2}-2$cm |
4.在Rt△ACB中,∠C=90°,下列式子成立的是( )
| A. | a=csinB | B. | a=bcosB | C. | c=asinB | D. | a=btanA |
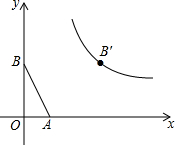 已知:如图,在平面直角坐标系中,点A(1,0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′恰在反比例函数y=$\frac{k}{x}$(x>0)的图象上.在同一平面内,是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF(即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=$\frac{k}{x}$(x>0)的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
已知:如图,在平面直角坐标系中,点A(1,0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′恰在反比例函数y=$\frac{k}{x}$(x>0)的图象上.在同一平面内,是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF(即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=$\frac{k}{x}$(x>0)的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.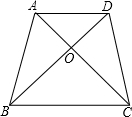 如图11,小强在纸上画出了两个三角形:△AOB与△DOC,点A,O,C在同一条直线上,点B,O,D在同一条直线上,且AB=DC,AC=DB.当他连接AD,BC后,得出了一个猜想:AD∥BC.你认为他的猜想正确吗?请说明理由.
如图11,小强在纸上画出了两个三角形:△AOB与△DOC,点A,O,C在同一条直线上,点B,O,D在同一条直线上,且AB=DC,AC=DB.当他连接AD,BC后,得出了一个猜想:AD∥BC.你认为他的猜想正确吗?请说明理由.