题目内容
11.如图①-③所示,在△ABC中,BD平分∠ABC.(1)如图①,DE⊥AB于E,DF⊥BC于F,求证:BD垂直平分EF.
(2)如图②,当有一点G从D点向B点运动时,GE⊥AB于E,GF⊥BC于F,此时(1)中的结论是否成立?请证明;
(3)如图③,当G点沿BD方向从D点沿BD延长线运动时,GE⊥AB于E,GF⊥BC(或其延长线)于F,此时(1)中的结论是否成立,不需证明.

分析 (1)由已知,BD是∠ABC的平分线,DE⊥AB于E,DF⊥BC于F,易证△BDF≌△BDE,可证BF=BE,从而可推出△BEF为等腰三角形,利用三线合一得出结论即可;
(2)类比(1)的方法证得△BGF≌△BGE,得出BF=BE,推出△BEF为等腰三角形,利用三线合一得出结论即可;
(3)类比(1)(2)证得△BGF≌△BGE,得出BF=BE,推出△BEF为等腰三角形,利用三线合一得出结论即可.
解答 证明:(1)在△ABC中,BD是∠ABC的平分线,DE⊥AB,DF⊥BC,
在△BDF和△BDE中,
$\left\{\begin{array}{l}{DE=DF}\\{BD=BD}\end{array}\right.$,
∴△BDE≌△BDF,
∴BE=BF,
∴BD⊥EF,且平分EF,
即BD垂直平分EF.
(2)BD垂直平分EF.
∵BD是∠ABC的平分线,GE⊥AB于E,GF⊥BC于F,
∴GE=GF,
在△BGF和△BGE中,
$\left\{\begin{array}{l}{GF=GE}\\{BG=BG}\end{array}\right.$,
∴△BGE≌△BGE,
∴BE=BF,
∴BD⊥EF,且平分EF,
即BD垂直平分EF.
(3)此时(1)中的结论仍然成立.
BD垂直平分EF.
∵BD是∠ABC的平分线,GE⊥AB于E,GF⊥BC于F,
∴GE=GF,
在△BGF和△BGE中,
$\left\{\begin{array}{l}{GF=GE}\\{BG=BG}\end{array}\right.$,
∴△BGE≌△BGE,
∴BE=BF,
∴BD⊥EF,且平分EF,
即BD垂直平分EF.
点评 此题考查三角形全等的判定与性质,角平分线的性质,等腰三角形的性质,利用三线合一是解决问题的关键.

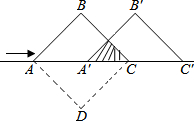 如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )
如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )| A. | 2cm | B. | $2\sqrt{2}+2$cm | C. | $\sqrt{2}$cm | D. | $2\sqrt{2}-2$cm |
| A. | 2160(1-x)2=1500 | B. | 1500(1+x)2=2160 | ||
| C. | 1500(1-x)2=2160 | D. | 1500+1500(1+x)+1500(1+x)2=2160 |
| A. | 1 | B. | 5 | C. | -5 | D. | -1 |
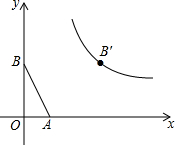 已知:如图,在平面直角坐标系中,点A(1,0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′恰在反比例函数y=$\frac{k}{x}$(x>0)的图象上.在同一平面内,是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF(即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=$\frac{k}{x}$(x>0)的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
已知:如图,在平面直角坐标系中,点A(1,0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′恰在反比例函数y=$\frac{k}{x}$(x>0)的图象上.在同一平面内,是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF(即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=$\frac{k}{x}$(x>0)的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.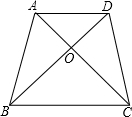 如图11,小强在纸上画出了两个三角形:△AOB与△DOC,点A,O,C在同一条直线上,点B,O,D在同一条直线上,且AB=DC,AC=DB.当他连接AD,BC后,得出了一个猜想:AD∥BC.你认为他的猜想正确吗?请说明理由.
如图11,小强在纸上画出了两个三角形:△AOB与△DOC,点A,O,C在同一条直线上,点B,O,D在同一条直线上,且AB=DC,AC=DB.当他连接AD,BC后,得出了一个猜想:AD∥BC.你认为他的猜想正确吗?请说明理由.