题目内容
18．
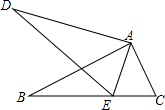如图，在△ABC和△ADE中，点E在BC边上，∠BAC=∠DAE，∠B=∠D，AB=AD．（1）求证：△ABC≌△ADE；
（2）若∠B=28°，∠BAC=90°，求∠AED的度数．
分析 （1）根据“ASA”直接判断两三角形全等；
（2）关键△ABC的内角和为180°，求出∠C的度数，再由△ABC≌△ADE，得到∠AED=∠C=62°．
解答 解：（1）在△ABC和△ADE中，
$\left\{\begin{array}{l}{∠BAC=∠DAE}\\{AB=AD}\\{∠B=∠D}\end{array}\right.$，
∴△ABC≌△ADE；
（2）∵在△ABC中，∠B=28°，∠BAC=90°，
∴∠C=180°-∠B-∠BAC=180°-28°-90°=62°，
∵△ABC≌△ADE，
∴∠AED=∠C=62°．
点评 本题考查了全等三角形的性质与判定，解决本题的关键是证明△ABC≌△ADE．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
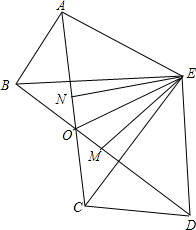如图，BE=CE，AB=DC，∠ABE=∠DCE，连接AC、DB交于点O，连接OE，EM、EN分别平分∠AEC和∠BED．求证：
